Lãi suất tiền gửi tiết kiệm của một số ngân hàng thời gian vừa qua liên tục thay

Gọi $a$ là số tháng gửi với lãi suất $0,75\% $ tháng, $x$ là số tháng gửi với lãi suất $0,8\% $/ tháng, khi đó số tháng gửi tiết kiệm là $a + 6 + x$, ($a,x \in $$\mathbb{N}$).
Số tiền cả vốn lẫn lãi là
$\begin{array}{l}
300 \times {1,0075^a} \times {1,012^6} \times {1,008^x} = 339,8996114\\
\Rightarrow {1,0075^a} \times {1,008^x} = 1,054742239\\
\Leftrightarrow a + x{\log _{1,0075}}\left( {1,008} \right) = {\log _{1,0075}}\left( {1,054742239} \right)\\
\Leftrightarrow a = {\log _{1,0057}}\left( {1,054742239} \right) - x{\log _{1,0075}}\left( {1,008} \right)
\end{array}$
Thử 1 số giá trị của $x:$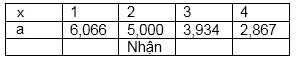

Vậy bác Minh gửi tiết kiệm trong thời gian $5 + 6 + 2 = 13$ tháng.