Số phức z = a + bi được biểu diễn trên mặt phẳng phức là tiếp điểm của một tiếp

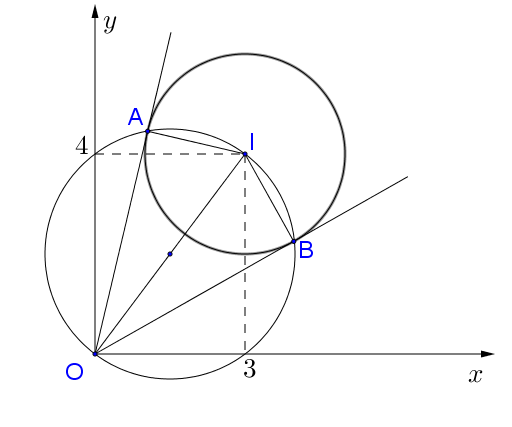
Gọi các tiếp điểm là $A$ và $B.$ Khi đó tọa độ $A,B$ được xác định là giao điểm của đường tròn $\left( C \right)$ và đường tròn đường kính $OI.$
Phương trình đường tròn đường kính $OI$ (tâm $I\left( {3;4} \right)$, bán kính bằng $\frac{5}{2}$):${\left( {x - \frac{3}{2}} \right)^2} + {\left( {y - 2} \right)^2} = \frac{{25}}{4}$
Do đó tọa độ các tiếp điểm là $\left\{ \begin{array}{l}
{\left( {x - 3} \right)^2} + {\left( {y - 4} \right)^2} = 4\\
{\left( {x - \frac{3}{2}} \right)^2} + {\left( {y - 2} \right)^2} = \frac{{25}}{4}
\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}
x = \frac{{63 - 8\sqrt {21} }}{{25}};\,\,y = \frac{{84 + 6\sqrt {21} }}{{25}}\\
x = \frac{{63 + 8\sqrt {21} }}{{25}};\,\,y = \frac{{84 - 6\sqrt {21} }}{{25}}
\end{array} \right.$
$ \Rightarrow \left| z \right| = \sqrt {21} .$