Cho hình chóp S.ABCD có đáy là hình vuông cạnh 2a và đường cao SA = asqrt 3 .

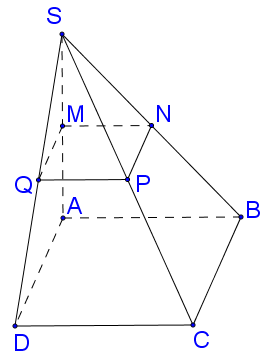
Ta có $mp\left( {MNPA} \right) \bot SA$ nên $mp\left( {MNPQ} \right)//mp\left( {ABCD} \right)$. Mặt khác $M$ là trung điểm của $SA$ nên $MN,NP,PQ,QM$ lần lượt là đường trung bình của các tam giác $SAB,SBC,SCD,SDA$. Do đó $MNPQ$ là hình vuông có cạnh bằng $a.$ Đường tròn ngoại tiếp hình vuông $MNPQ$ có đường kính bằng $MP = a\sqrt 2$, do đó bán kính $R = \frac{{a\sqrt 2 }}{2}.$
Thể tích của khối trụ cần tính bằng:
$V = \pi {R^2}.h = \pi {R^2}.MA = \pi .{\left( {\frac{{a\sqrt 2 }}{2}} \right)^2}.\frac{{a\sqrt 3 }}{2} = \frac{{\sqrt 3 \pi {a^3}}}{4}$.