Cho tứ diện ABCD có các cạnh AB,AC,AD đôi một vuông góc với nhau AB = 3,AC = 4,

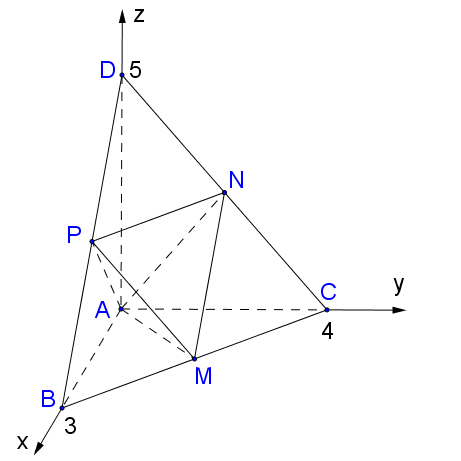
Ta có$AB,AC,AD$ đôi một vuông góc với nhau, do đó chọn hệ trục tọa độ $Oxyz$ như hình vẽ.
Khi đó, $A\left( {0;0;0} \right),M\left( {\frac{3}{2};2;0} \right),N\left( {0;2;\frac{5}{2}} \right),P\left( {\frac{3}{2};0;\frac{5}{2}} \right)$.
${V_{AMNP}} = \frac{1}{6}\left| {\left[ {\overrightarrow {AM} ,\overrightarrow {AN} } \right].\overrightarrow {AP} } \right| = \frac{{5}}{2}.$