Với giá trị nào của m thì phương trình sqrt x + 3 + 2sqrt 2 - x = m có nghiệm

TXĐ: $x \in \left[ { - 3;2} \right].$
Đạo hàm $y' = \frac{1}{{2\sqrt {x + 3} }} - \frac{1}{{\sqrt {2 - x} }} = \frac{{\sqrt {2 - x} - 2\sqrt {x + 3} }}{{2\sqrt {2 - x} .\sqrt {x + 3} }},$
$y' = 0 \Leftrightarrow \sqrt {2 - x} = 2\sqrt {x + 3} \Leftrightarrow 2 - x = 4\left( {x + 3} \right) \Leftrightarrow - 5x - 10 = 0 \Leftrightarrow x = - 2$ (thỏa mãn)
Bảng biến thiên: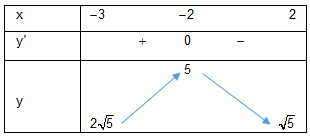

Từ bảng biến thiên suy ra phương trình đã cho có nghiệm duy nhất $ \Leftrightarrow \left[ \begin{array}{l}
m = 5\\
\sqrt 5 \le m < 2\sqrt 5
\end{array} \right..$