Gọi S là tập hợp những điểm biểu diễn số phức z thỏa mãn left| z - 1 - i right|

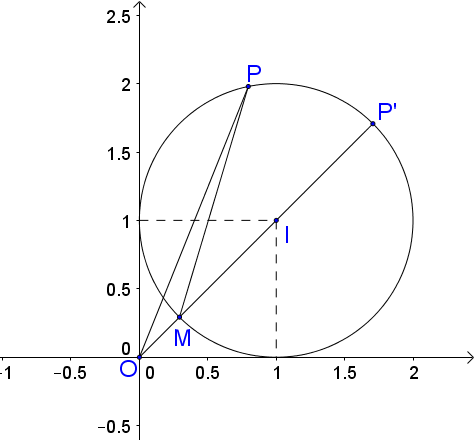
Gọi $z = x + iy,\,\,\,(x,y \in \mathbb{R} ).$
$\left| {z - 1 - i} \right| = 1 \Leftrightarrow \left| {x + iy - 1 - i} \right| = 1 \Leftrightarrow {\left( {x - 1} \right)^2} + {\left( {y - 1} \right)^2} = {1^2}\,\,\,\left( C \right).$
Gọi I là tâm của đường tròn $\left( C \right)$.
Với mọi điểm $P$ bất kì chạy trên $S$, ta có $OP \le OM + MP$, dó đó số phức tương ứng với P có môđun lớn nhất khi và chỉ khi $OP$ lớn nhất $ \Leftrightarrow OP = OM + MP \Leftrightarrow $ 3 điểm $O,M,P$ thẳng hàng và $M$ nằm giữa $O$ và $P$$ \Leftrightarrow P \equiv P'\,\,\,\left( {{x_P} > 1} \right)$
Phương trình đường thẳng $OI$: $y = x$. Tọa độ $P'$ là nghiệm của hệ phương trình:
$\left\{ \begin{array}{l}
{\left( {x - 1} \right)^2} + {\left( {y - 1} \right)^2} = 1\\
y = x
\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}
2{\left( {x - 1} \right)^2} = 1\\
y = x
\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}
y = x = 1 + \frac{1}{{\sqrt 2 }}\\
y = x = 1 - \frac{1}{{\sqrt 2 }}\,\,\left( {loai} \right)
\end{array} \right. \Rightarrow P'\left( {1 + \frac{{\sqrt 2 }}{2};1 + \frac{{\sqrt 2 }}{2}} \right).$
Suy ra $OP = \sqrt {{{\left( {1 + \frac{1}{{\sqrt 2 }}} \right)}^2} + {{\left( {1 + \frac{1}{{\sqrt 2 }}} \right)}^2}} = \sqrt {3 + 2\sqrt 2 } = \sqrt 2 + 1.$
Vậy số phức tương ứng với P có môđun lớn nhất bằng $\sqrt 2 + 1.$