Tìm tất cả các giá trị của tham số m để hàm số y=x3+3 x2-m x+1 đồng biến trên

Tập xác định: $D= \mathbb{R}$.

Hàm số đồng biến trên khoảng (-\infty ; 0) khi và chỉ khi $y^{\prime} \geq 0, \forall x<0$

$\Leftrightarrow 3 x^{2}+6 x-m \geq 0, \forall x<0$

Giải

$3 x^{2}+6 x-m \geq 0, \forall x<0 \Leftrightarrow 3 x^{2}+6 x \geq m, \forall x<0$

Xét hàm số $f(x)=3 x^{2}+6 x$ trên khoảng $(-\infty ; 0),$ ta có:

$f^{\prime}(x)=6 x+6 .$ Xét $f^{\prime}(x)=0 \Leftrightarrow 6 x+6=0 \Leftrightarrow x=-1 .$ Ta có $f(-1)=-3 .$

Bảng biến thiên: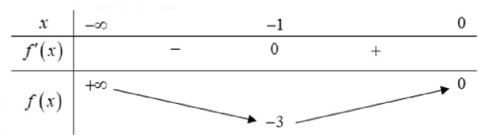



Dựa vào bảng biến thiên, ta có:$m \leq-3$