Tỉ số thể tích hình cầu và thể tích hình trụ cùng ngoại tiếp một hình lập phương

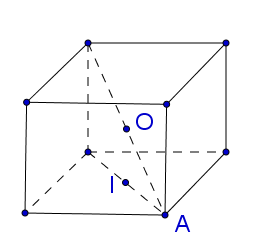
$O,\,\,I$ lần lượt là tâm mặt cầu ngoại tiếp hình lập phương và tâm đường tròn đáy của hình trụ ngoại tiếp hình lập phương.
Dễ dàng tính được bán kính mặt cầu ngoại tiếp ${R_1} = OA = \frac{{\sqrt 3 a}}{2},$ bán kính đáy của hình trụ ${R_2} = \frac{{\sqrt 2 a}}{2}.$
Ta có ${V_1} = \frac{4}{3}\pi {R_1}^3 = \frac{4}{3}\pi .\frac{{3\sqrt 3 {a^3}}}{8} = \frac{{\sqrt 3 \pi {a^3}}}{2}.$
${V_2} = \pi {R_2}^2.h = \pi {\left( {\frac{{\sqrt 2 a}}{2}} \right)^2}.a = \frac{{\pi {a^3}}}{2}.$
Vậy $\frac{{{V_1}}}{{{V_2}}} = \sqrt 3 .$