Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, hai mặt phẳng left( SAC

$\left\{ \begin{array}{l} \left( {SBD} \right) \bot \left( {ABCD} \right)\\ \left( {SAC} \right) \bot \left( {ABCD} \right)\\ \left( {SBD} \right) \cap \left( {{\rm{SA}}C} \right) = SO \end{array} \right. \Rightarrow SO \bot \left( {ABCD} \right).$
Ta có $d\left( {AB,\,\,SD} \right) = d\left( {A,\,\,\left( {SCD} \right)} \right) = 2d\left( {O,\,\,\left( {SCD} \right)} \right) \Rightarrow d\left( {O,\,\,\left( {SCD} \right)} \right) = \frac{{a\sqrt 3 }}{2}.$
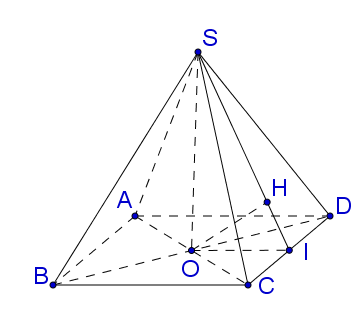
Trong mặt phẳng $\left( {ABCD} \right),$ kẻ $OI \bot CD.$ Trong mặt phẳng $\left( {SOI} \right)$, kẻ $OH \bot SI\,\,\left( 1 \right).$
$\left\{ \begin{array}{l} CD \bot OI\\ CD \bot SO \end{array} \right. \Rightarrow CD \bot \left( {SOI} \right) \Rightarrow CD \bot OH\,\,\left( 2 \right).$
Từ $\left( 1 \right),\,\,\left( 2 \right)$ ta có $OH \bot \left( {SCD} \right).$
Xét tam giác vuông $SOI$ có $\frac{1}{{O{H^2}}} = \frac{1}{{S{O^2}}} + \frac{1}{{O{I^2}}} \Rightarrow \frac{1}{{S{O^2}}} = \frac{1}{{O{H^2}}} - \frac{1}{{O{I^2}}} = \frac{4}{{3{a^2}}} - \frac{1}{{{a^2}}} = \frac{1}{{3{a^2}}} \Rightarrow SO = \sqrt 3 a.$
Vậy thể tích $S.ABCD$ là $V = \frac{1}{3}{S_{ABCD}}.SO = \frac{1}{3}.a.2a.\sqrt 3 a = \frac{{2\sqrt 3 {a^3}}}{3}.$