Cho hình chóp S.ABC có ABC là tam giác vuông cân tại B, AB = BC = 2a, widehat

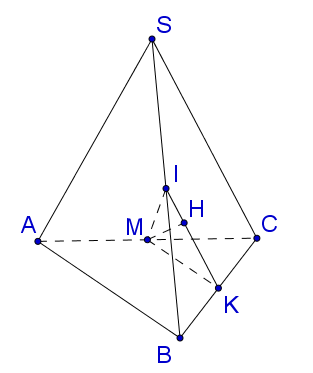
Gọi $K$ là trung điểm của $BC$.
Do $\widehat {SCB} = \widehat {SAB} = {90^o}$ nên dễ dàng nhận thấy trung điểm $I$ của $SB$ là tâm mặt cầu ngoại tiếp chóp $SABC.$
Gọi $M$ là trung điểm của $AC$. Tam giác $ABC$ vuông tại $B$, ta có $MA = MB = MC$, mặt khác $IA = IB = IC$, do đó $IM$ là trục của đường tròn ngoại tiếp tam giác $ABC$ hay $IM \bot \left( {ABC} \right).$
Ta có $d\left( {M,\,\,\left( {SBC} \right)} \right) = \frac{1}{2}d\left( {A,\,\,\left( {SBC} \right)} \right) = \frac{a}{{\sqrt 2 }}.$
Trong tam giác $IMK$, kẻ $MH \bot IK\,\,\left( 1 \right)$.
$\left\{ \begin{array}{l}
BC \bot IM\\
BC \bot MK
\end{array} \right. \Rightarrow BC \bot \left( {IMK} \right) \Rightarrow BC \bot MH\,\,\left( 2 \right).$
Từ $\left( 1 \right),\,\,\left( 2 \right)$ suy ra $MH \bot \left( {SBC} \right).$
Xét tam giác vuông $IMK$ ta có
$\begin{array}{l}
\frac{1}{{M{H^2}}} = \frac{1}{{M{I^2}}} + \frac{1}{{M{K^2}}}\\
\Leftrightarrow \frac{1}{{{{\left( {\frac{a}{{\sqrt 2 }}} \right)}^2}}} = \frac{1}{{M{I^2}}} + \frac{1}{{{a^2}}}\\
\Leftrightarrow \frac{1}{{M{I^2}}} = \frac{2}{{{a^2}}} - \frac{1}{{{a^2}}} = \frac{1}{{{a^2}}} \Rightarrow MI = a.
\end{array}$
Xét tam giác vuông $IMA$ ta có $IA = \sqrt {I{M^2} + M{A^2}} = \sqrt {{a^2} + {{\left( {\frac{{AC}}{2}} \right)}^2}} = \sqrt {{a^2} + {{\left( {\frac{{\sqrt 2 .2a}}{2}} \right)}^2}} = \sqrt 3 a.$
Vậy diện tích mặt cầu ngoại tiếp chóp $SABC$ là $S = 4\pi {R^2} = 4\pi {\left( {\sqrt 3 a} \right)^2} = 12\pi {a^2}.$