Cho tam giác vuông cân ABC với AB = AC = a. Khi quay tam giác đó (cùng với phần

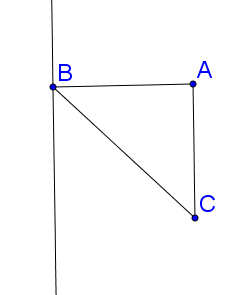
Thể tích khối tròn thu được bằng hiệu thể tích hình trụ bán kính kính đáy $AB$ chiều cao $AC$ trừ cho thể tích nón đỉnh $B$bán kính đáy $AB$ chiều cao $AC.$
${V_{tru}} = \pi {R^2}h = \pi A{B^2}AC = \pi {a^3}.$
${V_{non}} = \frac{1}{3}\pi {R^2}h = \frac{1}{3}\pi A{B^2}.AC = \frac{1}{3}\pi {a^3}.$
Vậy thể tích khối tròn tạo thành là $V = {V_{tru}} - {V_{non}} = \pi {a^3} - \frac{1}{3}\pi {a^3} = \frac{2}{3}\pi {a^3}.$