Cho tam giác vuông ABC với cạnh huyền BC = a. Mặt cầu đi qua ba điểm A,B,C có

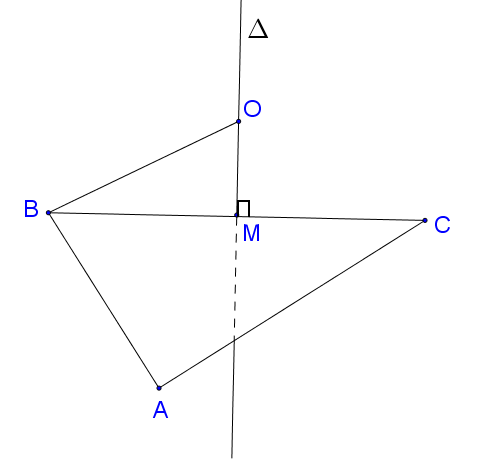
Gọi $M$ là trung điểm $BC$, kẻ đường thẳng $\Delta$ đi qua $M$ và vuông góc với mặt phẳng $\left( {ABC} \right)$. Khi đó $\Delta$ chính là trục của đường tròn ngoại tiếp đa giác đáy.
Suy ra tâm $O$ của mặt cầu đi qua $A,B,C$ nằm trên đường thẳng $\Delta$.
Gọi $R = OB$ là bán kính của mặt cầu, vì $OB \ge MB$ nên mặt cầu có bán kính nhỏ nhất là $R = MB = \frac{a}{2}.$