Cho hình chóp S.ABCD có đáy là hình chữ nhật, các mặt left( SAB right) và left(

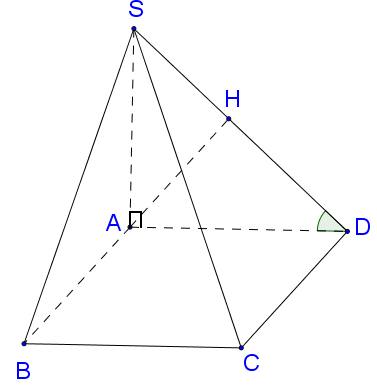
Ta có $\left( {SAB} \right)$ và $\left( {SAD} \right)$ cùng vuông góc với $\left( {ABCD} \right)$ $\Rightarrow SA \bot \left( {ABCD} \right).$
$\left\{ \begin{array}{l} CD \bot AD\\ CD \bot SA \end{array} \right. \Rightarrow CD \bot \left( {SAD} \right) \Rightarrow CD \bot SD$
Vì $SD \bot CD$ và $AD \bot CD$ $\Rightarrow$ $\left( {\left( {SCD} \right),\left( {ABCD} \right)} \right) = \widehat {SDA} = {60^0}$.
Kẻ $AH \bot SD,$ có $\left\{ \begin{array}{l} AH \bot SD\\ AH \bot CD,\,\,\,\left( {do\,\,CD \bot \left( {SAD} \right)} \right) \end{array} \right. \Rightarrow AH \bot \left( {SCD} \right) \Rightarrow d\left( {A,\left( {SCD} \right)} \right) = AH.$
Ta có $d\left( {AB,SC} \right) = d\left( {AB,\left( {SCD} \right)} \right) = d\left( {A,\left( {SCD} \right)} \right) = AH.$
$SA = AD.\tan {60^0} = a\sqrt 3 ,$ $\frac{1}{{A{H^2}}} = \frac{1}{{A{S^2}}} + \frac{1}{{A{D^2}}} \Rightarrow AH = \frac{{a\sqrt 3 }}{2}.$