Cho hình nón đỉnh S có đường tròn đáy bán kính bằng a, nội tiếp trong hình vuông

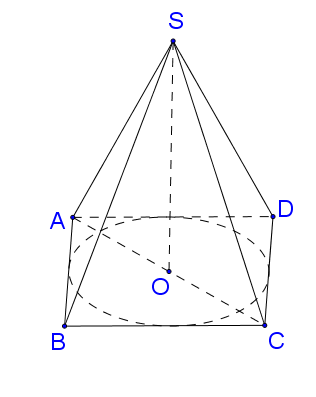
Đường tròn đáy nội tiếp hình vuông $ABCD,$ thì đường kính đáy bằng cạnh của hình vuông $ABCD.$ Khi đó cạnh hình vuông bằng $2a.$
Kí hiệu như hình vẽ, $OA = \frac{{2a\sqrt 2 }}{2} = a\sqrt 2 .$
$SO = \sqrt {S{A^2} - O{A^2}} = \sqrt {4{a^2} - 2{a^2}} = a\sqrt 2 $
$V = \frac{1}{3}.a\sqrt 2 .{\left( {2a} \right)^2} = \frac{{4{a^3}\sqrt 2 }}{3}$.