Áp dụng tính chất:
Cho mặt phẳng $\left( \alpha \right),$ đường thẳng $MN$ cắt mặt phẳng $\left( \alpha \right)$ tại $O$ thì
$\frac{{d\left( {M,\left( \alpha \right)} \right)}}{{d\left( {N,\left( \alpha \right)} \right)}} = \frac{{OM}}{{ON}}.$"
Ta có $\frac{{d\left( {A,\left( {SBD} \right)} \right)}}{{d\left( {C,\left( {SBD} \right)} \right)}} = \frac{{OA}}{{OC}} = 1 \Rightarrow d\left( {C,\left( {SBD} \right)} \right) = a\sqrt 3 .$
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, cạnh bên SA vuông góc với
Xuất bản: 21/08/2020 - Cập nhật: 21/08/2020 - Tác giả: Chu Huyền
Câu Hỏi:
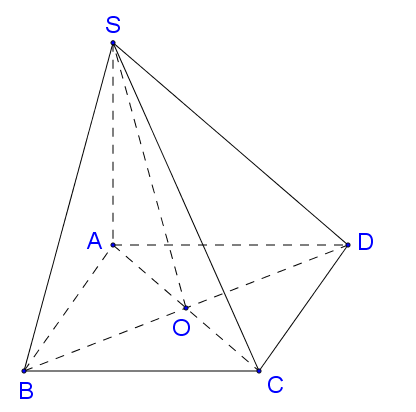
Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình chữ nhật, cạnh bên $SA$ vuông góc với đáy. Biết khoảng cách từ $A$ đến mặt phẳng $\left( {SBD} \right)$ bằng $a\sqrt 3 .$ Tính khoảng cách từ $C$ đến mặt phẳng $\left( {SBD} \right)$.
Câu hỏi trong đề: Đề ôn luyện thi THPT Quốc gia môn Toán số 2 có đáp án
Đáp án và lời giải
đáp án đúng: A
