Theo bài ra $\widehat {SBA} = {30^o}.$
Vậy $SA = AB.\tan {30^o} = \frac{a}{{\sqrt 3 }}.$
${V_{SABCD}} = \frac{1}{3}{S_{ABCD}}.SA = \frac{1}{3}.\frac{1}{2}\left( {AD + BC} \right).AB.SA = \frac{1}{6}.\left( {2a + a} \right).a.\frac{a}{{\sqrt 3 }} = \frac{{\sqrt 3 {a^3}}}{6}.$
${V_{SABD}} = \frac{1}{3}.{S_{ABD}}.SA = \frac{1}{3}.\frac{1}{2}AD.AB.SA = \frac{1}{6}.a.2a.\frac{a}{{\sqrt 3 }} = \frac{{\sqrt 3 {a^3}}}{9}.$
$\frac{{{V_{SABD}}}}{{{V_{SABCD}}}} = \frac{{\sqrt 3 {a^3}}}{9}.\frac{6}{{\sqrt 3 {a^3}}} = \frac{2}{3}.$
Vậy $\frac{{{V_{SABD}}}}{{{V_{SBCD}}}} = 2.$
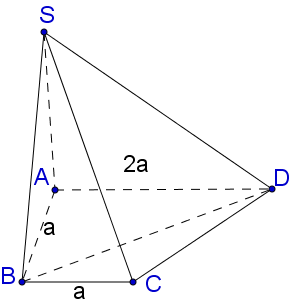
Cho hình chóp S.ABCD có đáy là hình thang vuông tại A và B , AD = 2a,,,AB = BC =
Xuất bản: 24/08/2020 - Cập nhật: 24/08/2020 - Tác giả: Chu Huyền
Câu Hỏi:
Cho hình chóp $S.ABCD$ có đáy là hình thang vuông tại $A$ và $B$ , $AD = 2a,\,\,AB = BC = a,\,\,SA$ vuông góc với đáy, $SB$ tạo với đáy một góc ${30^o}.$ Tính tỉ số thể tích $\frac{{{V_{SABD}}}}{{{V_{SBCD}}}}?$
Câu hỏi trong đề: Đề ôn luyện thi THPT Quốc gia môn Toán số 3 có đáp án
Đáp án và lời giải
đáp án đúng: C
