Cho hàm số y=f(x). Hàm số y=fprime(x) có đồ thị như hình vẽ. Hàm số

Ta có $g^{\prime}(x)=2 x \cdot f^{\prime}\left(x^{2}-2\right)=0$

$\Leftrightarrow\left[\begin{array}{l}x=0 \\ f\left(x^{2}-2\right)=0\end{array} \Leftrightarrow\left[\begin{array}{l}x=0 \\ x^{2}-2=-1 \\ x^{2}-2=2\end{array} \Leftrightarrow\left[\begin{array}{l}x=0 \\ x=\pm 1 \\ x=\pm 2\end{array}\right.\right.\right.$

Từ đồ thị $f^{\prime}(x)$ ta có $f^{\prime}\left(x^{2}-2\right)>0 \Leftrightarrow x^{2}-2>0 \Leftrightarrow\left[\begin{array}{l}x>2 \\ x<-2\end{array}\right.$

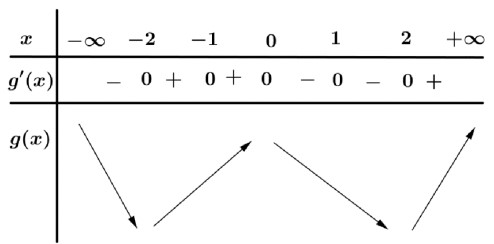
BBT

<#>

Từ BBT ta thấy đáp án C sai