Cho hàm số y=f(x) có đạo hàm liên tục trên mathbbR. Biết hàm số y=fprime(x) có

Ta có $g^{\prime}(x)=f^{\prime}(x+m) .$ Vì $y=f^{\prime}(x)$ liên tục trên

<#>

nên $g^{\prime}(x)=f^{\prime}(x+m)$ cũng liên tục trên $\mathbb{R}$

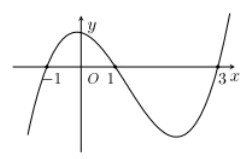
Căn cứ vào đồ thị hàm số $y=f^{\prime}(x)$ta thấy

$g^{\prime}(x)<0 \Leftrightarrow f^{\prime}(x+m)<0 \Leftrightarrow\left[\begin{array}{l}x+m<-1 \\ 1
Hàm số $g(x)=f(x+m)$nghịch biến trên khoảng $(1 ; 2)$

$\Leftrightarrow\left[\begin{array}{l}2 \leq-1-m \\ \left\{\begin{array}{l}3-m \geq 2 \\ 1-m \leq 1\end{array}\right.\end{array} \Leftrightarrow\left[\begin{array}{l}m \leq-3 \\ 0 \leq m \leq 1\end{array}\right.\right.$

Mà m là số nguyên thuộc đoạn $[-5 ; 5]$ nên ta có $S=\{-5 ;-4 ;-3 ; 0 ; 1\}$