Một tấm kim loại hình chữ nhật có tổng chiều dài và chiều rộng là 18,,cm. Người

Gọi chiều rộng của hình chữ nhật ban đầu là $x\,\,\left( {cm} \right)$, $0 < x < 18$.
$ \Rightarrow $ Chiều dài của hình chữ nhật ban đầu là $18 - x\,\,\,\left( {cm} \right)$
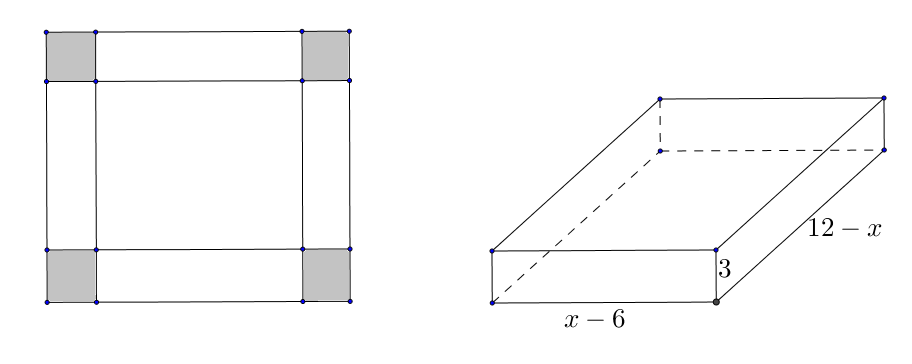
Hình hộp tạo thành có chiều dài là $18 - x - 6 = 12 - x$ $\left( {cm} \right)$, chiều rộng là $x - 6$$\left( {cm} \right)$ và chiều cao là $3\,\,\left( {cm} \right)$. Do đó thể tích của hình hộp là
$V = 3\left( {x - 6} \right)\left( {12 - x} \right) = 3\left( { - {x^2} + 18x - 72} \right)$
Xét hàm số $y = f\left( x \right) = 3\left( { - {x^2} + 18x - 72} \right)$:
$f'\left( x \right) = 3\left( { - 2x + 18} \right)\,,\,\,\,f'\left( x \right) = 0 \Leftrightarrow x = 9.$
Bảng biến thiên: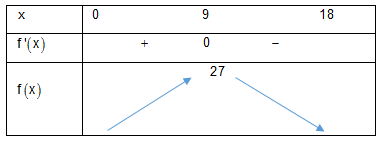

Từ bảng biến thiên suy ra thể tích lớn nhất ${V_{\max }} = 27 \Leftrightarrow x = 9.$