Ta có
$\begin{array}{l}
\frac{{SH}}{{SO}} = \frac{{SC}}{{SB}}\\
\Rightarrow SC = \frac{{SH.SB}}{{SO}} = \frac{{\left( {h - x} \right)\sqrt {{R^2} + {h^2}} }}{h}\\
\Rightarrow HC = S{C^2} - S{H^2} = \frac{{{R^2} + {h^2}}}{{{h^2}}}{\left( {h - x} \right)^2} - {\left( {h - x} \right)^2}.
\end{array}$
Ta có ${V_{tru}} = \pi .H{C^2}.OH = \pi \left( {\frac{{{h^2} + {R^2}}}{{{h^2}}} - 1} \right){\left( {h - x} \right)^2}.x.$
$V'\left( x \right) = \pi \left( {\frac{{{h^2} + {R^2}}}{{{h^2}}} - 1} \right)\left( {3{x^2} - 4hx + {h^2}} \right) = 0 \Leftrightarrow x = \frac{h}{3}.$
Vậy thể tích lớn nhất của hình trụ là ${V_{tru\left( {\max } \right)}} = \pi \left( {\frac{{{h^2} + {R^2}}}{{{h^2}}} - 1} \right){\left( {h - \frac{h}{3}} \right)^2}.\frac{h}{3} = \pi .\frac{{{R^2}}}{{{h^2}}}.\frac{{4{h^2}}}{9}.\frac{h}{3} = \frac{{4\pi {R^2}h}}{{27}}.$
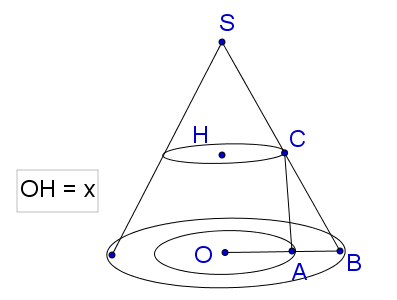
Một nóc tòa nhà cao tầng có dạng hình nón. Người ta muốn xây một bể nước có dạng
Xuất bản: 24/08/2020 - Cập nhật: 24/08/2020 - Tác giả: Chu Huyền
Câu Hỏi:
Một nóc tòa nhà cao tầng có dạng hình nón. Người ta muốn xây một bể nước có dạng một hình trụ nội tiếp trong hình nón để chứa nước (như hình vẽ minh họa). Cho biết $SO = h;\,\,\,OB = R;\,\,OH = x\,\,\left( {0 < x < h} \right).$ Tìm thể tích lớn nhất của hình trụ.

Câu hỏi trong đề: Đề ôn luyện thi THPT Quốc gia môn Toán số 3 có đáp án
Đáp án và lời giải
đáp án đúng: B
