Ta có:$y^{\prime}=3\left[f^{\prime}(x+2)-\left(x^{2}-3\right)\right]$
Với $x \in(-1 ; 0) \Rightarrow x+2 \in(1 ; 2) \Rightarrow f^{\prime}(x+2)>0,$ lại có $x^{2}-3<0 \Rightarrow y^{\prime}>0 ; \forall x \in(-1 ; 0)$
Vậy hàm số $y=3 f(x+2)-x^{3}+3 x$ đồng biến trên khoảng $(-1 ; 0)$.
Vậy hàm số $y=3 f(x+2)-x^{3}+3 x$ đồng biến trên khoảng $(-1 ; 0)$.
Chú ý:
+) Ta xét $x \in(1 ; 2) \subset(1 ;+\infty) \Rightarrow x+2 \in(3 ; 4) \Rightarrow f^{\prime}(x+2)<0 ; x^{2}-3>0$
Suy ra hàm số nghịch biến trên khoảng (1;2)nên loại hai phương án A,D.
+) Tương tự ta xét $x \in(-\infty ;-2) \Rightarrow x+2 \in(-\infty ; 0) \Rightarrow f^{\prime}(x+2)<0 ; x^{2}-3>0 \Rightarrow y^{\prime}<0 ; \forall x \in(-\infty ;-2)$
Suy ra hàm số nghịch biến trên khoảng ($-\infty ;-2$)nên loại hai phương án B
Cho hàm số f(x) có bảng xét dấu của đạo hàm như sauHàm số y=3 f(x+2)-x3+3 x đồng
Xuất bản: 01/02/2021 - Cập nhật: 01/02/2021 - Tác giả: Nguyễn Hưng
Câu Hỏi:
Cho hàm số $f(x)$ có bảng xét dấu của đạo hàm như sau
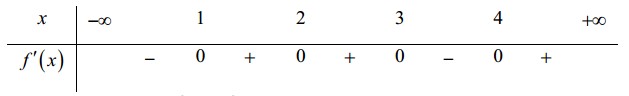
Hàm số $y=3 f(x+2)-x^{3}+3 x$ đồng biến trên khoảng nào dưới đây?
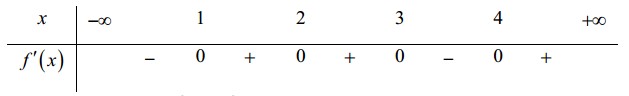
Hàm số $y=3 f(x+2)-x^{3}+3 x$ đồng biến trên khoảng nào dưới đây?
Đáp án và lời giải
đáp án đúng: C
