Ta có : $y^{\prime}=-2 f^{\prime}(1-x)+\frac{x}{\sqrt{x^{2}+1}}-1=-2 f^{\prime}(1-x)+\frac{x-\sqrt{x^{2}+1}}{\sqrt{x^{2}+1}}$
Chú ý : $\frac{x-\sqrt{x^{2}+1}}{\sqrt{x^{2}+1}}<0, \forall x \in R$.
+) Vói $x \in(-\infty ; 1) \Rightarrow 1-x \in(0 ;+\infty)$ (loại vì không thể kết luận được)
+) Vói $x \in(-\infty ;-2) \Rightarrow 1-x \in(3 ;+\infty)$ (loại vì không thể kết luận được) +) Vói $x \in(-3 ;-2) \Rightarrow 1-x \in(3 ; 4)$ (loai vì không thể kết luận được)
+) Với $x \in(-2 ; 0) \Rightarrow 1-x \in(1 ; 3) \Rightarrow f^{\prime}(1-x) \geq 0 \Rightarrow y^{\prime}<0$ (thỏa mãn).
Cho hàm số f(x) có bảng xét dấu của đạo hàm như sau :Hàm số y=2
Xuất bản: 01/02/2021 - Cập nhật: 01/02/2021 - Tác giả: Nguyễn Hưng
Câu Hỏi:
Cho hàm số $f(x)$ có bảng xét dấu của đạo hàm như sau :
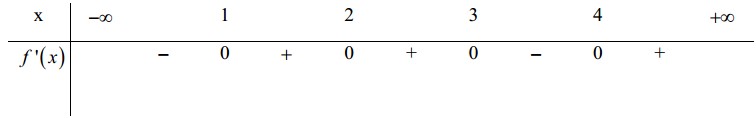
Hàm số $y=2 f(1-x)+\sqrt{x^{2}+1}-x$ nghịch biến trên khoảng nào dưới đây ?
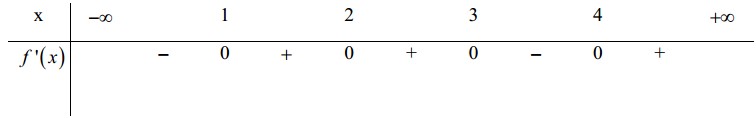
Hàm số $y=2 f(1-x)+\sqrt{x^{2}+1}-x$ nghịch biến trên khoảng nào dưới đây ?
Đáp án và lời giải
đáp án đúng: C
