Cho hai số thực dương x,y thỏa mãn x + y = 1. Giá trị nhỏ nhất của A = 2x +

Ta có $x + y = 1 \Leftrightarrow y = 1 - x$ khi đó $A = {2^x} + \frac{2}{{27}}{.4^{2 - x}}$.
Đặt ${2^x} = t,\,\,\,\left( {t > 0} \right)$ ta được $A = t + \frac{{32}}{{27{t^2}}}$.
Vì $x,y$ là các số thực dương nên $y = 1 - x > 0 \Leftrightarrow x \in \left( {0;1} \right)$, suy ra $t \in \left( {1;2} \right)$.
Xét hàm số $A = f\left( t \right) = t + \frac{{32}}{{27{t^2}}}$ với $t \in \left( {1;2} \right)$:
Đạo hàm $f'\left( t \right) = 1 - \frac{{64}}{{27{t^3}}} = \frac{{27{t^3} - 64}}{{{t^3}}}$, $f'\left( t \right) = 0 \Leftrightarrow t = \frac{4}{3}$.
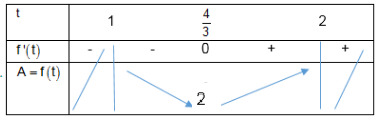
BBT:

Vậy ${A_{\min }} = 2 \Leftrightarrow x = {\log _2}\frac{4}{3}.$