Một nhà sản xuất cần thiết kế một thùng sơn dạng hình trụ có nắp đậy với dung

Đổi $20$ lít $= 20\,000\,\,c{m^3}.$
Gọi bán kính nắp đậy của thùng sơn là $x$ $\left( {cm} \right)$, $x > 0$, chiều cao của thùng sơn là $h\,\,\left( {cm} \right)$.
Khi đó thể tích của thùng sơn là $V = \pi {x^2}h = 20\,000 \Rightarrow h = \frac{{20\,000}}{{\pi {x^2}}}.$
Diện tích toàn phần của thùng sơn là ${S_{tp}} = 2\pi x h + 2\pi {x^2} = \frac{{40\,000}}{{{x}}} + 2\pi {x^2}$
Để nhà sản xuất tiết kiệm được vật liệu nhất tức là ${S_{tp}}$ nhỏ nhất.
Ta có $S' = - \frac{{40\,000}}{x^2} + 4\pi x$,
$S' = 0 \Leftrightarrow - \frac{{40000}}{x^2} + 4\pi x = 0 \Leftrightarrow 4\pi {x^3} = 40000 \Leftrightarrow {x^3} = \frac{{10000}}{\pi } \Rightarrow \left[ \begin{array}{l} x = \sqrt[3]{{\frac{{10000}}{\pi }}}\\ x = - \sqrt[3]{{\frac{{10000}}{\pi }}} \end{array} \right..$
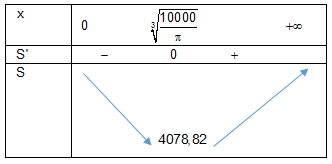
Bảng biến thiên:


Vậy bán kính nắp đậy là $\sqrt[3]{{\frac{{10000}}{\pi }}}$ thì sẽ tiết kiệm vật liệu nhất.