Ta có điểm $A\left( {0; - 1} \right),\,\,B\left( {2;1} \right);\,\,\,C\left( { - 1;1} \right)$. Gọi $D\left( {a;b} \right)$, khi đó $ABCD$ là hình bình hành
$ \Leftrightarrow \overrightarrow {AB} = \overrightarrow {DC} \Leftrightarrow \left( {2;2} \right) = \left( { - 1 - a;1 - b} \right) \Leftrightarrow \left\{ \begin{array}{l}
a = - 3\\
b = - 1
\end{array} \right.$, suy ra số phức $z$ biểu diễn $D$ là $z = - 3 - i.$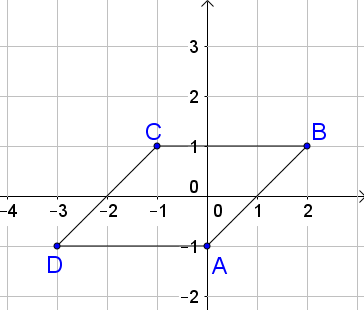
Trong mặt phẳng phức cho các điểm A,B,C theo thứ tự biểu diễn các số phức z_1 =
Xuất bản: 24/08/2020 - Cập nhật: 24/08/2020 - Tác giả: Chu Huyền
Câu Hỏi:
Trong mặt phẳng phức cho các điểm $A,B,C$ theo thứ tự biểu diễn các số phức ${z_1} = - i;\,\,{z_2} = 2 + i;\,\,{z_3} = - 1 + i$. Tìm số phức $z$ biểu diễn điểm $D$ sao cho tứ giác $ABCD$ là hình bình hành.
Câu hỏi trong đề: Đề ôn luyện thi THPT Quốc gia môn Toán số 4 có đáp án
Đáp án và lời giải
đáp án đúng: B
