Gọi ${z_1} = x + iy,\,\,\,x,y \in $$\mathbb{R}$. Khi đó điểm biểu diễn số phức ${z_1}$ là $M\left( {x;y} \right)$ thỏa mãn
$\left| {x + iy - 3} \right| = 2 \Leftrightarrow {\left( {x - 3} \right)^2} + {y^2} = 4$ do đó tập hợp các điểm biểu diễn số phức ${z_1}$ là đường tròn tâm $I\left( {3;0} \right)$ bán kính $R = 2.$
Ta có ${z_2} = i{z_1} = i\left( {x + iy} \right) = - y + ix$. Khi đó điểm biểu diễn số phức ${z_2}$ là $N\left( { - y;x} \right)$.
Ta có $\left| {{z_1} - {z_2}} \right| = \left| {\overrightarrow {OM} - \overrightarrow {ON} } \right| = \left| {\overrightarrow {NM} } \right| = MN$.
Nhận thấy $\overrightarrow {OM} .\overrightarrow {ON} = 0$ và $OM = ON$ do đó tam giác $MON$ vuông cân tại $O.$
$MN = OM\sqrt 2 $ nên $MN$ nhỏ nhất $ \Leftrightarrow $ OM nhỏ nhất $ \Leftrightarrow M \equiv M'$ ($M'$ là giao điểm của $OI$ với đường tròn về phía bên trái như hình vẽ). Tức là $M\left( {1;0} \right).$ Khi đó $MN = \sqrt{2}OM = \sqrt{2}.1 = \sqrt{2}.$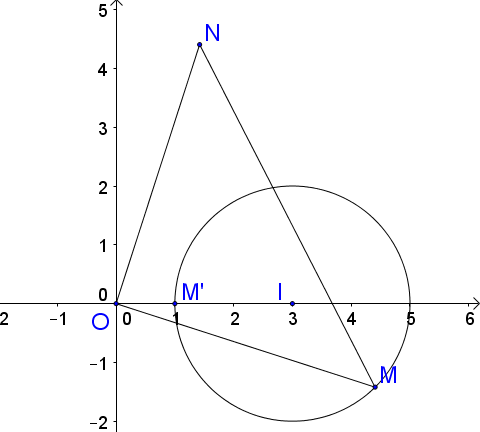
Cho hai số phức z_1,z_2 thỏa mãn left| z_1 - 3 right| = 2 và z_2 = iz_1. Tìm giá
Xuất bản: 24/08/2020 - Cập nhật: 24/08/2020 - Tác giả: Chu Huyền
Câu Hỏi:
Cho hai số phức ${z_1},{z_2}$ thỏa mãn $\left| {{z_1} - 3} \right| = 2$ và ${z_2} = i{z_1}$. Tìm giá trị nhỏ nhất của $\left| {{z_1} - {z_2}} \right|.$
Câu hỏi trong đề: Đề ôn luyện thi THPT Quốc gia môn Toán số 4 có đáp án
Đáp án và lời giải
đáp án đúng: A
