Từ đồ thị hàm số $g = f'\left( x \right)$ta thấy: hàm số $f'\left( x \right) = 0$ tại hai điểm phân biệt $x = - 2$ và $x = 1.$
Mặt khác, tại $x = 1$ thì $f'\left( x \right)$ đổi dấu từ dương sang âm, do đó hàm số $y = f\left( x \right)$ đạt cực đại tại $x = 1.$
Hàm số y = fleft( x right) xác định, liên tục trên khoảng K và có đạo hàm
Xuất bản: 24/08/2020 - Cập nhật: 24/08/2020 - Tác giả: Chu Huyền
Câu Hỏi:
Hàm số $y = f\left( x \right)$ xác định, liên tục trên khoảng $K$ và có đạo hàm $f'\left( x \right)$ trên $K.$ Biết hình vẽ sau đây là của đồ thị hàm số $f'\left( x \right)$ trên $K.$
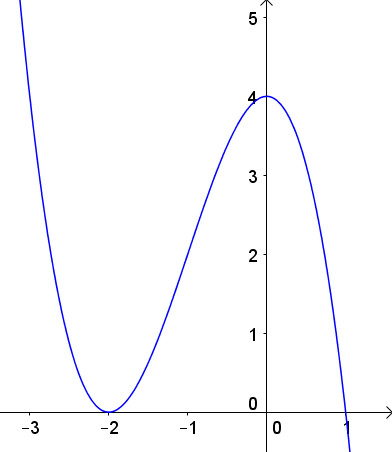
Khẳng định nào sau đây là đúng?

Khẳng định nào sau đây là đúng?
Câu hỏi trong đề: Đề ôn luyện thi THPT Quốc gia môn Toán số 4 có đáp án
Đáp án và lời giải
đáp án đúng: A
