Đồ thị hàm số y = left| x3 right| - 3x2 + 1 có bao nhiêu điểm cực trị?

Xét hàm số $y = {x^3} - 3{x^2} + 1$:
Tập xác định: $D = $$\mathbb{R}.$
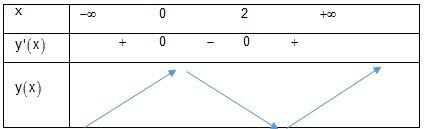
Đạo hàm $y' = 3{x^2} - 6x\,;\,\,\,y' = 0 \Leftrightarrow \left[ \begin{array}{l}
x = 0\\
x = 2
\end{array} \right.$.
Bảng biến thiên:

Hàm số $y = \left| {{x^3}} \right| - 3{x^2} + 1 = \left\{ \begin{array}{l}
{x^3} - 3{x^2} + 1\,,\,\,\,\,\,x \ge 0\\
- {x^3} - 3{x^3} + 1\,,\,\,\,\,\,x < 0
\end{array} \right.$ là hàm số chẵn và đồ thị của nó được suy ra từ đồ thị hàm số $y = {x^3} - 3{x^2} + 1$ bằng cách bỏ đi phần bên trái trục tung. Giữ nguyên phần bên phải trục tung và lấy đối xứng với phần bên phải $Oy$ qua $Oy.$
Như vậy ta sẽ được đồ thị hàm số $y = \left| {{x^3}} \right| - 3{x^2} + 1$ có dạng như sau:

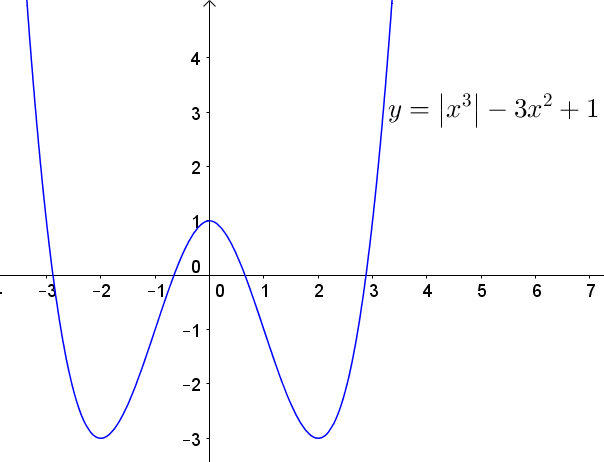
Vậy đồ thị hàm số $y = \left| {{x^3}} \right| - 3{x^2} + 1$ có ba điểm cực trị.