Cho tứ diện đều ABCD cạnh a . Thể tích của khối tứ diện ABCD là

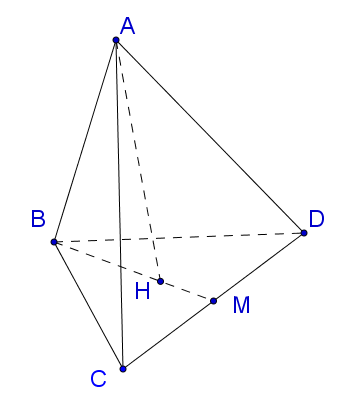
Gọi $M$ là trung điểm của $CD$ , $H$ là trọng tâm của tam giác $BCD$ .
Ta có
$AH \bot \left( {BCD} \right)$ (giả thiết $ABCD$ là tứ diện đều) suy ra ${V_{ABCD}} = \frac{1}{3}{S_\Delta }_{BCD}.AH.$
Trong $\Delta BCD$ : $CD = a,\,\,BM = \frac{{\sqrt 3 a}}{2}$suy ra ${S_{\Delta BCD}} = \frac{1}{2}.CD.BM = \frac{1}{2}.a.\frac{{\sqrt 3 a}}{2} = \frac{{\sqrt 3 {a^2}}}{4}.$
Trong $\Delta ABH$ : $AB = a,\,\,BH = \frac{2}{3}BM = \frac{2}{3}.\frac{{\sqrt 3 a}}{2} = \frac{{\sqrt 3 a}}{3}$ suy ra $AH = \sqrt {A{B^2} - B{H^2}} = \sqrt {{a^2} - \frac{{{a^2}}}{3}} = \frac{{\sqrt 2 a}}{{\sqrt 3 }}.$
Vậy ${V_{ABCD}} = \frac{1}{3}{S_\Delta }_{BCD}.AH = \frac{1}{3}.\frac{{\sqrt 3 {a^2}}}{4}.\frac{{\sqrt 2 a}}{{\sqrt 3 }} = \frac{{\sqrt 2 {a^3}}}{{12}}.$