Cho hình chóp SABC , Delta ABC vuông cân tại A, SA bot left( ABC right) , BC =

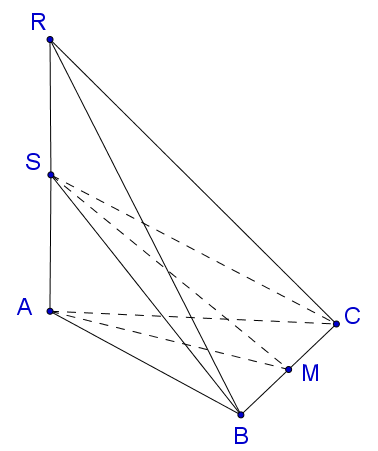
Gọi $M$ là trung điểm của $BC$ . Dễ thấy $\widehat {SMA} = {45^o}.$
Tam giác $ABC$ vuông cân tại $A$ suy ra $AB = AC = \frac{a}{{\sqrt 2 }}$, $AM = \frac{{BC}}{2} = \frac{a}{2}$ .
Tam giác $SAM$ vuông tại $A$ , $\widehat {SMA} = {45^o}$ suy ra $SA = AM = \frac{a}{2}.$
Vậy ${V_{SABC}} = \frac{1}{3}.{S_{ABC}}.SA = \frac{1}{3}.\frac{1}{2}.AB.AC.SA = \frac{1}{6}.\frac{a}{{\sqrt 2 }}.\frac{a}{{\sqrt 2 }}.\frac{a}{2} = \frac{{{a^3}}}{{24}}.$
Mà ${V_{RABC}} = \frac{1}{3}.{S_{ABC}}.RA = \frac{1}{3}.{S_{ABC}}.\left( {RS + SA} \right) = 3.{V_{SABC}} = \frac{{{a^3}}}{8}.$