Kẻ $AH \bot BD \Rightarrow BD \bot \left( {SAH} \right) \Rightarrow \left( {SBD} \right) \bot \left( {SAH} \right)$
Kẻ $AK \bot SH \Rightarrow AK \bot \left( {SBD} \right) \Rightarrow d\left( {A,\left( {SBD} \right)} \right) = AK$
Ta có $\frac{1}{{A{H^2}}} = \frac{1}{{A{B^2}}} + \frac{1}{{A{D^2}}} = \frac{1}{{{a^2}}} + \frac{1}{{4{a^2}}} = \frac{5}{{4{a^2}}}$.
$SA = AD\tan {60^0} = 2a\sqrt 3 $.
$\frac{1}{{A{K^2}}} = \frac{1}{{A{S^2}}} + \frac{1}{{A{H^2}}} = \frac{1}{{12{a^2}}} + \frac{5}{{4{a^2}}} = \frac{4}{{3{a^2}}} \Rightarrow AK = \frac{{a\sqrt 3 }}{2}.$
Cho hình chóp S.ABCD, đáy ABCD là hình chữ nhật. Cạnh SA vuông góc với mặt phẳng
Xuất bản: 21/08/2020 - Cập nhật: 21/08/2020 - Tác giả: Chu Huyền
Câu Hỏi:
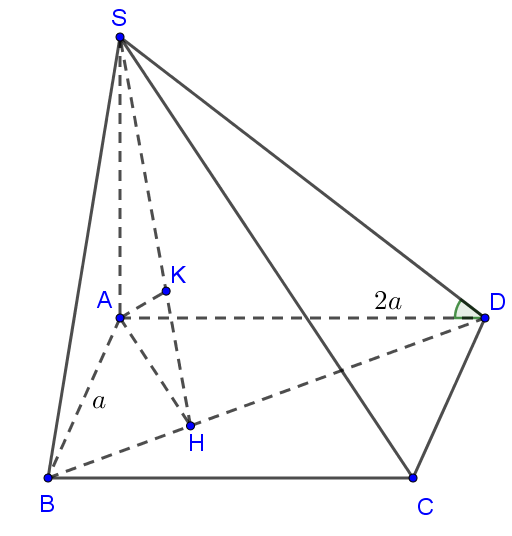
Cho hình chóp S.ABCD, đáy ABCD là hình chữ nhật. Cạnh SA vuông góc với mặt phẳng (ABCD). Biết $AB = a,AD = 2a$, góc giữa cạnh bên SD và mp(ABCD) bằng ${60^0}$. Tính khoảng cách từ A đến mp(SBD).
Câu hỏi trong đề: Luyện thi THPT Quốc gia môn Toán số 1 có đáp án
Đáp án và lời giải
đáp án đúng: C
