Cho hình trụ tròn xoay có hai đáy là hai hình tròn left( O;R right),,,left( O';R

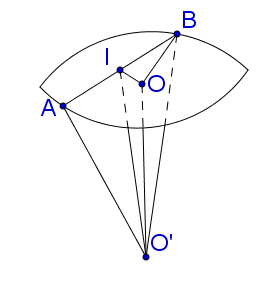
Gọi $I$ là trung điểm của $AB$, ta có $\widehat {O'IO} = {60^o}.$
Đặt $OI = x$ ta có
$\begin{array}{l}
{\rm{OO}}' = x.\tan {60^o}\\
IO' = \frac{x}{{\cos {{60}^o}}} = 2x\\
AI = IO'.\cot \widehat {IAO'} = 2x.cot{60^o} = \frac{{2x}}{{\sqrt 3 }}.
\end{array}$
Mà $A{I^2} + O{I^2} = {R^2} \Leftrightarrow \frac{{4{x^2}}}{3} + {x^2} = {R^2} \Leftrightarrow x = \frac{{\sqrt 3 R}}{{\sqrt 7 }}.$
Vậy ${\rm{OO}}' = x.\tan {60^o} = \frac{{\sqrt 3 R}}{{\sqrt 7 }}.\tan {60^o} = \frac{{3R}}{{\sqrt 7 }}$.
Vậy ${S_{xq}} = 2\pi R.\frac{{3R}}{{\sqrt 7 }} = \frac{{6\pi \sqrt 7 {R^2}}}{7}.$