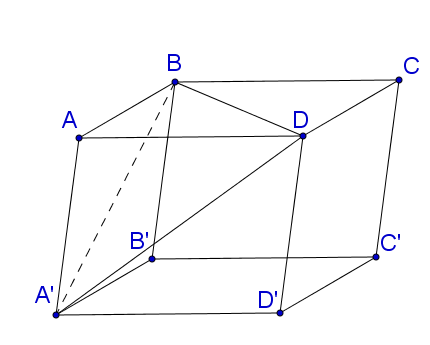
${V_{A'ABD}} = \frac{1}{3}{S_{ABD}}.d\left( {A',\left( {ABD} \right)} \right) .$
${V_{ABCD.A'B'C'D'}} = {S_{ABCD}}.d\left( {A',\left( {ABCD} \right)} \right) = 2{S_{ABD}}.d\left( {A',\left( {ABD} \right)} \right)$ .
Vậy $\frac{{{V_{A'ABD}}}}{{{V_{ABCD.A'B'C'D'}}}} = \frac{1}{6}.$
Cho khối hộp ABCD.A'B'C'D' . Tính tỉ số thể tích của khối tứ diện ABDA' và khối
Xuất bản: 21/08/2020 - Cập nhật: 21/08/2020 - Tác giả: Chu Huyền
Câu Hỏi:
Cho khối hộp $ABCD.A'B'C'D'$ . Tính tỉ số thể tích của khối tứ diện $ABDA'$ và khối hộp $ABCD.A'B'C'D'.$
Câu hỏi trong đề: Luyện thi THPT Quốc gia môn Toán số 1 có đáp án
Đáp án và lời giải
đáp án đúng: B
