Cho hình chóp tứ giác đều có cạnh đáy bằng a, mặt bên tạo với mặt đáy một góc

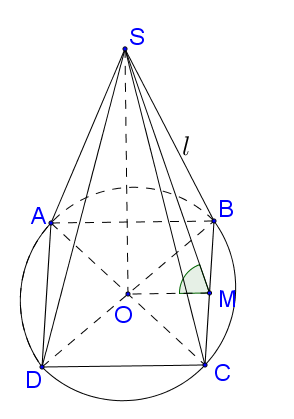
Gọi $M$ là trung điểm của $BC$, suy ra $\left\{ \begin{array}{l}
BC \bot MS\\
BC \bot OM
\end{array} \right. \Rightarrow \left( {\left( {SBC} \right),\left( {ABCD} \right)} \right) = \widehat {SMO} = {60^0}$.
$SO = OM.\tan {60^0} = \frac{{a\sqrt 3 }}{2}.$
Gọi $\ell $, $R$ lần lượt là đường sinh, và bán kính của hình nón ngoại tiếp hình chóp, khi đó
$\ell = SB = \sqrt {S{O^2} + O{B^2}} = \sqrt {{{\left( {\frac{{a\sqrt 3 }}{2}} \right)}^2} + {{\left( {\frac{{a\sqrt 2 }}{2}} \right)}^2}} = \frac{{a\sqrt 5 }}{2}$, $R = OB = \frac{{a\sqrt 2 }}{2}.$
Diện tích xung quanh của hình nón ngoại tiếp hình chóp là
${S_{xq}} = \pi R\ell = \pi .\frac{{a\sqrt 2 }}{2}.\frac{{a\sqrt 5 }}{2} = \frac{{\pi {a^2}\sqrt {10} }}{4}.$