Gọi $M$ là trung điểm của $AA'$. Gọi $V$ là thể tích của hình lăng trụ $ABC.A'B'C'$.
Khi đó $\frac{{{V_1}}}{{{V_2}}} = \frac{{\frac{V}{2} - {V_{AMEF}}}}{{\frac{V}{2} + {V_{AMEF}}}}.$
Mà $\frac{{{V_{AMEF}}}}{V} = \frac{{\frac{1}{3}{S_{MEF}}.AM}}{{{S_{ABC}}.AA'}} = \frac{1}{3}.\frac{1}{2} = \frac{1}{6}.$
Do đó $\frac{{{V_1}}}{{{V_2}}} = \frac{{\frac{V}{2} - \frac{V}{6}}}{{\frac{V}{2} + \frac{V}{6}}} = \frac{1}{2}.$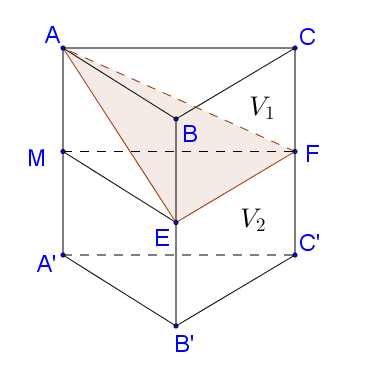
Cho hình lăng trụ ABC.A'B'C'. Gọi E,F lần lượt là trung điểm của BB' và CC'. Mặt
Xuất bản: 24/08/2020 - Cập nhật: 24/08/2020 - Tác giả: Chu Huyền
Câu Hỏi:
Cho hình lăng trụ $ABC.A'B'C'$. Gọi $E,F$ lần lượt là trung điểm của $BB'$ và $CC'$. Mặt phẳng $\left( {AEF} \right)$ chia khối lăng trụ thành hai phần có thể tích ${V_1}$ và ${V_2}$ như hình vẽ. Khi đó tỉ số $\frac{{{V_1}}}{{{V_2}}}$ có giá trị là
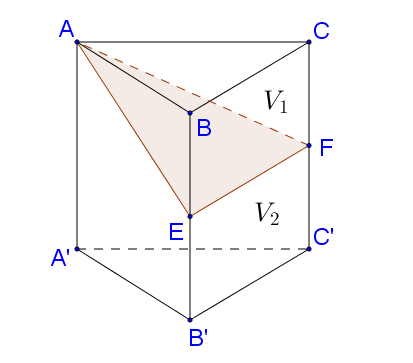

Câu hỏi trong đề: Đề ôn luyện thi THPT Quốc gia môn Toán số 4 có đáp án
Đáp án và lời giải
đáp án đúng: B
