Cho hàm số y = sqrt 2 - x2 . Gọi M và m lần lượt là giá trị lớn nhất và giá trị

Tập xác định: $ - \sqrt 2 \le x \le \sqrt 2 .$
Đạo hàm $y' = \frac{{ - x}}{{\sqrt {2 - {x^2}} }},\,\,y' = 0 \Leftrightarrow x = 0.$
Bảng biến thiên: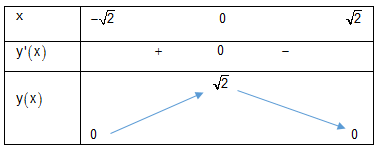

Từ bảng biến thiên suy ra $M = {y_{\max }} = \sqrt 2 \Leftrightarrow x = 0;\,\,$ $m = {y_{\min }} = 0 \Leftrightarrow x = \pm \sqrt 2 .$
Do đó $M - 2m = \sqrt 2 - 2.0 = \sqrt 2 .$