Cho hai đường thẳng a,b cố định, song song với nhau và khoảng cách giữa chúng

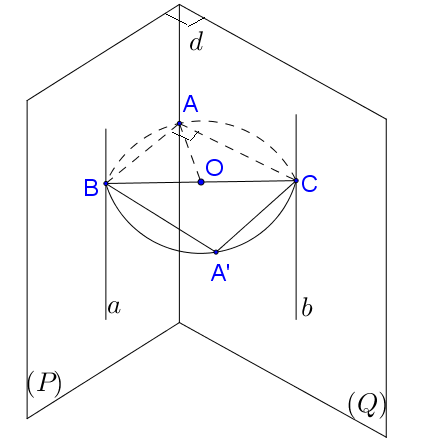
Lấy $A$ là một điểm bất kì thuộc $d.$ Từ $A$ kẻ $\left\{ \begin{array}{l} AB \bot d,\,\,B \in a\\ AC \bot d,\,\,C \in b \end{array} \right..$
Vì $\left( P \right) \bot \left( Q \right) \Rightarrow \widehat {BAC} = {90^0}.$ (1)
Ta đi chứng minh $BC$ chính là khoảng cách giữa hai đường thẳng $a$ và $b$, $BC = 4:$
Ta có $\left\{ \begin{array}{l} AB \bot d\\ AC \bot d \end{array} \right. \Rightarrow d \bot \left( {ABC} \right) \Rightarrow d \bot BC$
Mà $a//b//d$ suy ra $BC \bot a,b \Rightarrow BC = 4.$ (2)
Từ $\left( 1 \right)\left( 2 \right)$ suy ra $A$ thuộc đường tròn đường kính $BC$ bằng $4$ không đổi.
Do đó $d$ thuộc mặt trụ có khoảng cách giữa đường sinh và trục bằng $2.$