Cho a > b > 0. Đường elip left( E right) có phương trình fracx2a2 + fracy2b2 =

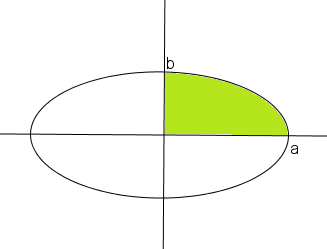
Xét hình phẳng $D$ giới hạn bởi các trục $Ox,\,\,Oy$ và đồ thị của hàm số $y = b\sqrt {1 - \frac{{{x^2}}}{{{a^2}}}} .$ Diện tích elip bằng $4$ lần diện tích hình phẳng $D.$
$S = 4\int_0^a {b\sqrt {1 - \frac{{{x^2}}}{{{a^2}}}} } dx.$ Đặt $\begin{array}{l}
x = a\sin t \Rightarrow dx = a\cos tdt.\\
S = 4\int_0^{\frac{\pi }{2}} {b\sqrt {1 - {{\sin }^2}t} } .a\cos tdt = 4ab\int_0^{\frac{\pi }{2}} {{{\cos }^2}t} dt = 4ab\int_0^{\frac{\pi }{2}} {\frac{{\left( {1 + \cos 2t} \right)}}{2}} dt = \left. {2abt} \right|_0^{\frac{\pi }{2}} + \left. {ab\sin 2t} \right|_0^{\frac{\pi }{2}} = \pi ab.
\end{array}$