Ta có
$\begin{array}{l}
z = 1 - 2i\\
z' = \frac{{1 - i}}{2}z = \frac{{\left( {1 - i} \right)\left( {1 - 2i} \right)}}{2} = \frac{{1 - 2i - i + 2{i^2}}}{2} = - \frac{1}{2} - \frac{3}{2}i.
\end{array}$
Biểu diễn điểm $M,\,\,\,M'$ trên hệ trục tọa độ $Oxy$
Ta có $\overrightarrow {OM'} = \left( { - \frac{1}{2}; - \frac{3}{2}} \right)$, $\overrightarrow {MM'} = \left( { - \frac{3}{2};\frac{1}{2}} \right)$. Nhận thấy $\overrightarrow {OM'} .\overrightarrow {MM'} = 0 \Rightarrow OM' \bot MM'.$
${S_{OMM'}} = \frac{1}{2}.OM'.MM' = \frac{1}{2}.\sqrt {{{\left( { - \frac{1}{2}} \right)}^2} + {{\left( { - \frac{3}{2}} \right)}^2}} .\sqrt {{{\left( { - \frac{3}{2}} \right)}^2} + {{\left( {\frac{1}{2}} \right)}^2}} = \frac{1}{2}.\frac{{\sqrt {10} }}{2}.\frac{{\sqrt {10} }}{2} = \frac{5}{4}.$ 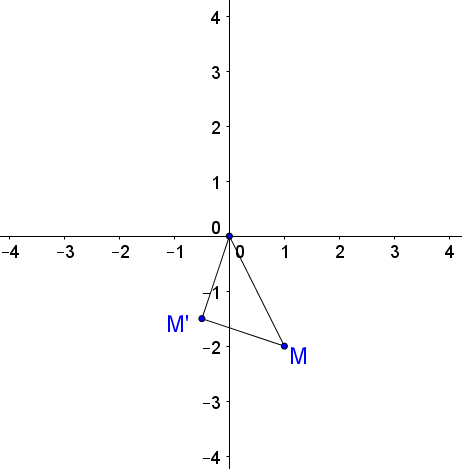
Trong mặt phẳng tọa độ Oxy, gọi M là điểm biểu diễn số phức z = 1 - 2i, N là
Xuất bản: 24/08/2020 - Cập nhật: 24/08/2020 - Tác giả: Chu Huyền
Câu Hỏi:
Trong mặt phẳng tọa độ $Oxy$, gọi $M$ là điểm biểu diễn số phức $z = 1 - 2i$, $N$ là điểm biểu diễn số phức $z' = \frac{{1 - i}}{2}z$. Tính diện tích tam giác $OMM'.$
Câu hỏi trong đề: Đề ôn luyện thi THPT Quốc gia môn Toán số 5 có đáp án
Đáp án và lời giải
đáp án đúng: B
