Ta có $f^{\prime}(x)=0 \Leftrightarrow\left[\begin{array}{l}x^{2}=0 \\ x-1=0 \\ (x-2)^{3}=0\end{array} \Leftrightarrow\left[\begin{array}{l}x=0 \\ x=1 \\ x=2\end{array}\right.\right.$
Bảng biến thiên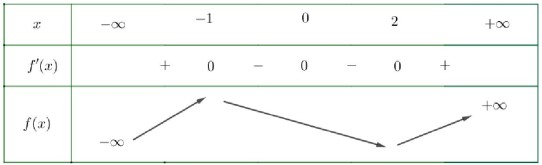
Dựa vào bảng biến thiên suy ra hàm số có 1 điểm cực đại.
Hàm số f(x) có đạo hàm fprime(x)=x2(x+1)(x-2)3, forall x in mathbbR .Hỏi f(x) có
Xuất bản: 02/02/2021 - Cập nhật: 02/02/2021 - Tác giả: Nguyễn Hưng
Câu Hỏi:
Hàm số $f(x)$ có đạo hàm $f^{\prime}(x)=x^{2}(x+1)(x-2)^{3}, \forall x \in \mathbb{R}$ .Hỏi $f(x)$ có bao nhiêu điểm cực đại?
Câu hỏi trong đề: Trắc nghiệm tìm cực trị của hàm số khi biết y, y’
Đáp án và lời giải
đáp án đúng: C
