Cho lăng trụ đứng ABC.A'B'C' có đáy là tam giác cân, AB = AC = 2a,,,widehat BAC

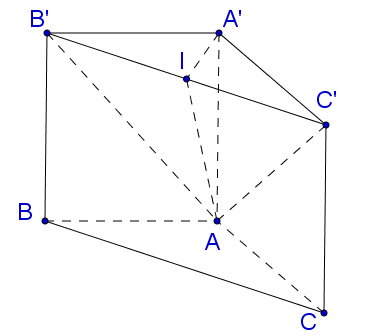
Gọi $I$ là trung điểm của $B'C'.$
Trong tam giác $A'B'C'$ ta có $\begin{array}{l} B'C{'^2} = A'B{'^2} + A'C{'^2} - 2.A'B'.A'C'.\cos \widehat {B'A'C'} = 4{a^2} + 4{a^2} - 2.2a.2a.cos{120^o} = 12{a^2}\\ \Rightarrow B'C' = 2\sqrt 3 a\\ \Rightarrow B'I = IC = \sqrt 3 a. \end{array}$
Trong tam giác $A'B'I$ ta có $A'I = \sqrt {A'B{'^2} - B'{I^2}} = \sqrt {{{\left( {2a} \right)}^2} - {{\left( {\sqrt 3 a} \right)}^2}} = a.$
Dễ dàng chứng minh được $\widehat {A'IA} = {60^o}.$ Trong tam giác $A'IA$ có $A'A = A'I.\tan {60^o} = a.\sqrt 3 = \sqrt 3 a.$
Thể tích lăng trụ đứng
$V = \frac{1}{2}B'C'.A'I.AA' = \frac{1}{2}.2a\sqrt 3 .a.a\sqrt 3 = 3{a^3}\left( {dvtt} \right).$