Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng 2a , góc giữa cạnh bên và mặt

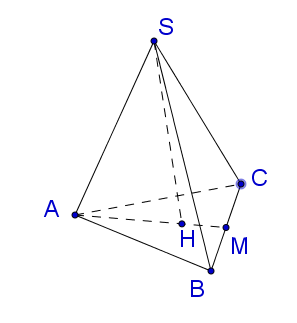
Gọi $H$ là trọng tâm tam giác $ABC$, vì $S.ABC$ là hình chóp tam giác đều nên $SH$ vuông góc với $(ABC)$.
Vậy $d(S,(ABC))=SH$. Theo bài ra ta có góc $\widehat {SAH} = {60^0}.$
Ta có $AM = \frac{{\sqrt 3 .2a}}{2} = a\sqrt 3 ,\,\,\,\,AH = \frac{2}{3}.a\sqrt 3 = \frac{{2\sqrt 3 a}}{3}.$
Trong tam giác vuông $SHA,\,\,SH = AH.\tan {60^o} = \frac{{2\sqrt 3 a}}{3}.\sqrt 3 = 2a.$