Cho hình chóp S.ABC có SA = 3, SA vuông góc với đáy. Tam giác ABC vuông tại A,

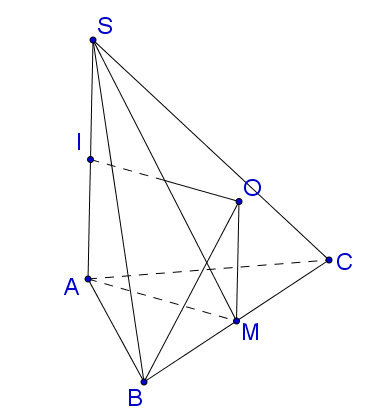
Gọi $M$ là trung điểm của $BC$. Trong mặt phẳng $\left( {SAM} \right)$, kẻ đường trung trực của đoạn thẳng $SA$ , qua điểm $M$ kẻ đường thẳng song song với $SA$ , hai đường thẳng đó cắt nhau tại $O$ .
Dễ dàng chứng minh được $O$ là tâm mặt cầu ngoại tiếp chóp $S.ABC$ .
Ta có $OB = \sqrt {O{M^2} + M{B^2}} = \sqrt {A{I^2} + M{B^2}} = \sqrt {{{\left( {\frac{3}{2}} \right)}^2} + {{\left( {\frac{5}{2}} \right)}^2}} = \frac{{\sqrt {17} }}{{\sqrt 2 }}.$
Diện tích mặt cầu ngoại tiếp
$S = 4\pi {\left( {\frac{{\sqrt {17} }}{{\sqrt 2 }}} \right)^2} = 34\pi \,\,\,\,\left( {dvdt} \right).$