Cho hình chóp S.ABC có SA = 8, SA vuông góc với đáy. Tam giác ABC vuông tại A,

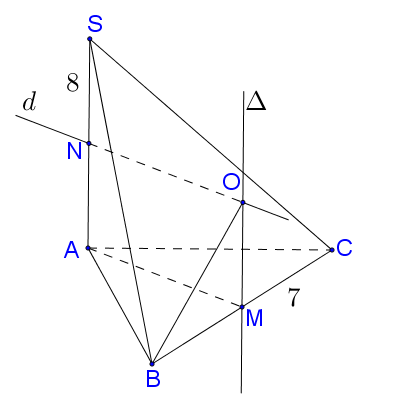
Gọi $M$ là trung điểm của $BC.$ Suy ra $M$ là tâm đường tròn ngoại tiếp tam giác vuông $ABC.$
Kẻ đường thẳng $\Delta$ đi qua $M$ và vuông góc với mặt phẳng $\left( {ABC} \right)$, $\Delta$ chính là trục của đường tròn ngoại tiếp đa giác đáy.
Trong mặt phẳng chứa $SA$ và $\Delta$, dựng đường trung trực $d$ của $SA.$ $d \cap \Delta = O$.
$O \in \Delta \Rightarrow OA = OB = OC,$ $O \in d \Rightarrow OA = OS$ do đó $O$ là tâm mặt cầu ngoại tiếp hình chóp $SABC.$
Bán kính $R = OB = \sqrt {O{M^2} + B{M^2}} = \sqrt {{4^2} + {{\left( {\frac{7}{2}} \right)}^2}} = \frac{{\sqrt {113} }}{2}.$