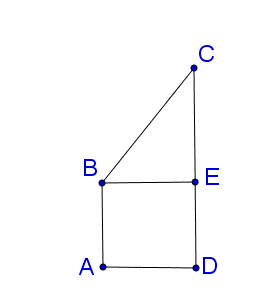
Khi quay hình thang quanh AB, ta được khối tròn quay có thể tích băng thể tích hình trụ bán kính đáy AD, chiều cao CD trừ đi thể tích hình nón có bán kính đáy AD, chiều cao CE.
Dễ dàng tính được CE = 1.
Ta có
$\begin{array}{l}
{V_{tru}} = \pi {1^2}.2 = 2\pi \left( {dvtt} \right)\\
{V_{non}} = \frac{1}{3}\pi {1^2}.1 = \frac{\pi }{3}\left( {dvtt} \right)
\end{array}$
Vậy thể tích khối tròn xoay thu được $V = 2\pi - \frac{\pi}{3} = \frac{{5\pi}}{3}\left({dvtt}\right)$.
Cho hình thang vuông ABCD có đường cao AD = 1, đáy nhỏ AB = 1, đáy lớn CD = 2.
Xuất bản: 24/08/2020 - Cập nhật: 02/11/2023 - Tác giả: Chu Huyền
Câu Hỏi:
Đáp án và lời giải
Khi quay hình chữ nhật một vòng quanh một cạnh cố định, ta được hình:
Khi quay hình chữ nhật một vòng quanh một cạnh cố định, ta được hình trụ.
Người ta dùng mấy hình chiếu để biểu diễn khối tròn xoay?
Người ta dùng 2 hình chiếu để biểu diễn khối tròn xoay.
Đối với khối tròn xoay, người ta thường dùng hai hình chiếu để biểu diễn:
Đối với khối tròn xoay, người ta thường dùng hai hình chiếu để biểu diễn, một hình chiếu thể hiện mặt bên và chiều cao, một hình chiếu thể hiện hình dạng và đường kính mặt đáy.
Cho tam giác ABC vuông tại A, AB = 6, AC = 8. Quay hình tam giác ABC xung quanh trục BC ta được một khối tròn xoay có thể tích là:
Khi quay tam giác theo BC ta sẽ có được hai khối nón như hình vẽ.
Trong $\Delta ABC$, gọi H là chân đường cao của A đến BC. Ta có:
$\begin{array}{l}
BC = \sqrt {A{B^2} + A{C^2}} = \sqrt {{6^2} + {8^2}} = 10.\\
A{B^2} = BH.BC \Rightarrow BH = \frac{{A{B^2}}}{{BC}} = \frac{{36}}{{10}} = 3,6.\\
Tính thể tích $V$ khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi các đường $y = \sqrt {\tan x}, y = 0, x = 0, x = \frac{\pi }{6}$ xung quanh trục Ox.
Thể tích khối tròn xoay tạo thành khi quay phần mặt phẳng được giới hạn như hình vẽ (tô màu) quanh trục Ox là
$V = \pi \int_0^{\frac{\pi }{6}} {{{\left( {\sqrt {\tan x} } \right)}^2}dx} = \pi \int_0^{\frac{\pi }{6}} {{\mathop{\rm tanx}\nolimits} } dx = \pi \int_0^{\frac{\pi }{6}} {\frac{{\sin x}}{{\cos x}}dx} = \left. { - \pi \ln \left| {\cos x} \right|} \right|_0^{\frac{\pi }{6}} = - \pi \ln \frac{{\sqrt 3 }}{2}.$
Cho a,b là hai số dương. Gọi K là hình phẳng nằm trong góc phần tư thứ hai, giới hạn bởi parabol $y = a{x^2}$ và đường thẳng y = - bx. Thể tích khối tròn xoay tạo được khi quay K xung quanh trục hoành là một số không phụ thuộc và giá trị của a và b nếu a và b thỏa mãn điều kiện sau:
Hoành độ giao điểm của đồ thị hàm số $y = a{x^2}$ và đồ thị hàm số $y = - bx$ là nghiệm của phương trình
$\begin{array}{l}
a{x^2} = - bx\\
\Leftrightarrow a{x^2} + bx = 0\\
\Leftrightarrow x\left( {ax + b} \right) = 0\\
\Leftrightarrow \left[ \begin{array}{l}
Cho hình phẳng $\left(H \right)$ giới hạn bởi các đường $y=sqrt{x}$, y=-x và x=3 Tính thể tích của khối tròn xoay tạo thành khi quay hình $\left(H \right)$ quanh trục hoành.
Phương trình hoành độ giao điểm là $\sqrt x = - x \Leftrightarrow \left\{ \begin{array}{l}
- x \ge 0\\
x = - {x^2}
\end{array} \right. \Leftrightarrow x = 0.$
Thể tích khối tròn xoay cần tìm là:
${V_{Ox}} = \pi \int\limits_0^3 {\left| {{x^2} - x} \right|dx = \pi \int\limits_0^1 {\left( { - {x^2} + x} \right)dx + } } \pi \int\limits_1^3 {\left( {{x^2} - x} \right)dx} = \left. {\pi \left( { - \frac{{{x^3}}}{3} + \frac{{{x^2}}}{2}} \right)} \right|_0^1 + \left. {\pi \left( {\frac{{{x^3}}}{3} - \frac{{{x^2}}}{2}} \right)} \right|_1^3 = \frac{\pi }{6} + \frac{{14\pi }}{3} = \frac{{29\pi }}{6}.$
Cho hình vuông $ABCD$ có cạnh $a,$ $M$ là trung điểm của $AD.$ Xét khối tròn xoay sinh bởi tam giác $CDM$ (cùng các điểm trong của nó) khi quay quanh đường thẳng $AB.$ Thể tích của khối tròn xoay đó bằng
Khi quay hình vuông ABCD quanh AB sinh ra mặt trụ có thể tích ${V_1} = \pi {a^3}$.
Hình thang AMCB sinh ra hình nón cụt có thể tích ${V_2} = \left( {\frac{1}{3}\pi {a^2}.SB} \right) - \left( {\frac{1}{3}\pi .\frac{{{a^2}}}{4}.SA} \right) = \frac{1}{3}\pi \left( {2{a^3} - \frac{{{a^3}}}{4}} \right) = \frac{{7\pi {a^3}}}{{12}}$.
Gọi D là miền phẳng giới hạn bởi đồ thị các hàm số $y = \sqrt{\cos x}$, y = 0, x = 0 và $x = \frac{\pi }{4}$. Tính thể tích của khối tròn xoay khi quay D quanh trục hoành.
Thể tích của khối tròn xoay tạo thành khi quay D quanh trục hoành là:
$V = \pi \int\limits_0^{\pi /4} {{y^2}dx} = \pi \int\limits_0^{\pi /4} {\cos xdx} = \left. {\pi \left( {{\mathop{\rm sinx}\nolimits} } \right)} \right|_0^{\pi /4} = \frac{{\pi \sqrt 2 }}{2}.$
