Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số y = 4x - x2 và y = x3 - 4.

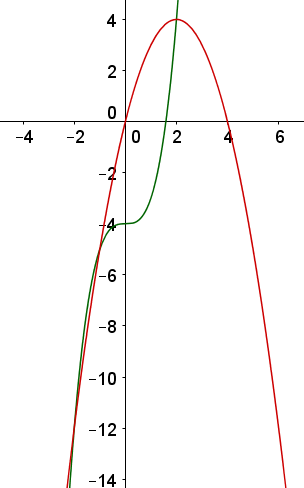
Hoành độ giao điểm của đồ thị hàm số $y = {x^3} - 4$ và đồ thị hàm số $y = 4x - {x^2}$ là nghiệm của phương trình
$\begin{array}{l}
{x^3} + {x^2} - 4x - 4 = 0\\
\Leftrightarrow {x^2}\left( {x + 1} \right) - 4\left( {x + 1} \right) = 0\\
\Leftrightarrow \left( {{x^2} - 4} \right)\left( {x + 1} \right) = 0\\
\Leftrightarrow \left[ \begin{array}{l}
x = - 2\\
x = - 1\\
x = 2
\end{array} \right..
\end{array}$
Diện tích hình phẳng
$\begin{array}{l}
S = \int\limits_{ - 2}^2 {\left| {{x^3} - 4 + {x^2} - 4x} \right|dx} = \int\limits_{ - 2}^{ - 1} {\left( {{x^3} - 4 + {x^2} - 4x} \right)dx + \int\limits_{ - 1}^2 {\left( { - {x^2} + 4x - {x^3} + 4} \right)dx} } \\
= \left. {\frac{{{x^4}}}{4}} \right|_{ - 2}^{ - 1} - \left. {4x} \right|_{ - 2}^{ - 1} + \left. {\frac{{{x^3}}}{3}} \right|_{ - 2}^{ - 1} - \left. {2{x^2}} \right|_{ - 2}^{ - 1} - \left. {\frac{{{x^3}}}{3}} \right|_{ - 1}^2 + \left. {2{x^2}} \right|_{ - 1}^2 - \left. {\frac{{{x^4}}}{4}} \right|_{ - 1}^2 + \left. {4x} \right|_{ - 1}^2\\
= \frac{{71}}{6}.
\end{array}$