Để giúp các em nắm vững kiến thức và học tốt hơn môn Toán lớp 7 , Đọc Tài Liệu gửi tới các bạn tài liệu lý thuyết trọng tâm và hướng dẫn giải chi tiết các bài tập bài tập hợp Q các số hữu tỉ.
Lý thuyết Tập hợp Q các số hữu tỉ
Số hữu tỉ
Số hữu tỉ là số viết được dưới dạng phân số \(\frac{a}{b}(a,b \in \mathbb{Z};b \ne 0)\)
Tập hợp các số hữu tỉ được kí hiệu là Q
Ví dụ: \(- 7,21;\frac{{ - 7}}{{ - 9}};\frac{0}{{ - 2}};2\frac{3}{8};...\) là các số hữu tỉ
Chú ý :
+ Các số thập phân đã biết đều là các số hữu tỉ. Các số nguyên, hỗn số cũng là các số hữu tỉ
+ Các phân số bằng nhau là các cách viết khác nhau của cùng một số hữu tỉ
Ví dụ: \(-\frac{9}{{30}} = \frac{{ - 3}}{{10}}\) nên 2 phân số \(- \frac{9}{{30}}\) và \(\frac{{ - 3}}{{10}}\) cùng biểu diễn 1 số hữu tỉ
Biểu diễn số hữu tỉ trên trục số
Ta có thể biểu diễn mọi số hữu tỉ trên trục số
Trên trục số, điểm biểu diễn số hữu tỉ a được gọi là điểm a.
Ta chọn phân số tối giản để biểu diễn số hữu tỉ.
Số đối của một số hữu tỉ
+ Mỗi số hữu tỉ đều có một số đối. Số đối của số hữu tỉ \(\frac{a}{b}\) là số hữu tỉ \(- \frac{a}{b}\)
Trên trục số, điểm biểu diễn số hữu tỉ a được gọi là điểm a.
Trên trục số, 2 điểm biểu diễn 2 số hữu tỉ đối nhau a và –a nằm về 2 phía khác nhau so với điểm O và có cùng khoảng cách đến O.
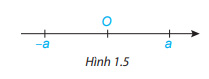
Ví dụ: -5 là số đối của 5
So sánh hai số hữu tỉ
- Ta có thể so sánh hai số hữu tỉ bất kì bằng cách viết chúng dưới dạng phân số rồi so sánh 2 phân số đó.
- Với 2 số hữu tỉ a và b bất kì, ta luôn có hoặc a = b, hoặc a < b, hoặc a > b
- Cho 3 số hữu tỉ a, b, c. Nếu a < b; b < c thì a < c ( Tính chất bắc cầu)
- Trên trục số, nếu a < b thì điểm a nằm trước điểm b
- Các số hữu tỉ lớn hơn 0 gọi là các số hữu tỉ dương.
- Các số hữu tỉ nhỏ hơn 0 gọi là các số hữu tỉ âm.
- Số 0 không là số hữu tỉ âm, cũng không là số hữu tỉ dương.
Chú ý: Trên trục số, các điểm nằm trước gốc O biểu diễn số hữu tỉ âm; các điểm nằm sau gốc O biểu diễn số hữu tỉ dương.
Cách so sánh hai số hữu tỉ:
Ta viết chúng về cùng dạng phân số (hoặc dạng số thập phân) rồi so sánh chúng.
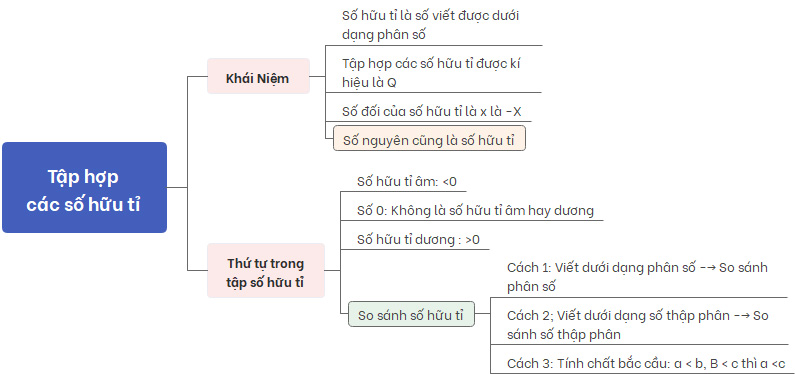
Sơ đồ tư duy Tập hợp Q các số hữu tỉ
Giải bài tập Tập hợp Q các số hữu tỉ Cánh diều
Hướng dẫn trả lời các câu hỏi trong bài và giải bài tập trang 10 và 11 SGK Toán 7 tập 1 Cánh Diều
Trả lời câu hỏi trong bài
Trả lời chi tiết các câu hỏi hoạt động và luyện tập trong bài
- Viết các số − 3 ; 0,5 ; 2 3/7 dưới dạng phân số
- Nhiệt độ lúc 13 giờ ngày 24/01/2016 tại một số trạm đo được...
- Các số 21 ; −12; −7/9 ; −4,7; −3,05 có là số hữu tỉ không
- Biểu diễn số hữu tỉ −0,3 trên trục số
- Quan sát hai điểm biểu diễn các số hữu tỉ − 5/4 và 5/4 trên trục số sau
- Tìm số đối của mỗi số sau: 2/9 ; −0,5
- Hoạt động 4 trang 9 Toán lớp 7 Tập 1
- So sánh –3,23 và – 3,32; −7/3 và –1,25
- Giả sử hai điểm a, b lần lượt biểu diễn hai số nguyên a, b trên trục số nằm ngang
Đáp án bài tập bài Tập hợp Q các số hữu tỉ
Đáp án chi tiết các bài tập trang 10 và trang 11 SGK Toán 7 tập 1 ( Cánh Diều )
Bài 1 trang 10
Các số \(13, -29; -2,1; 2,28; \frac{{ - 12}}{{ - 18}}\) có là số hữu tỉ vì:
\(13 = \frac{{13}}{1}; - 29 = \frac{{ - 29}}{1}; - 2,1 = \frac{{21}}{{10}};2,28 = \frac{{228}}{{100}} = \frac{{54}}{{25}};\frac{{ - 12}}{{ - 18}} = \frac{2}{3}\)
Chú ý: Một số nguyên cũng là một số hữu tỉ.
Bài 2 trang 10
- a) \( \in \)
- b) \(\notin\)
- c) \(\notin\)
- d) \( \in \)
- e) \( \in \)
- g) \( \in \)
Bài 3 trang 10
a) Đúng
b) Đúng
c) Sai. Vì a là số hữu tỉ thì chưa chắc a là số tự nhiên.
d) Sai. Vì a là số hữu tỉ thì chưa chắc a là số nguyên.
e) Sai. Vì các số tự nhiên là các số hữu tỉ
g) Sai. Vì các số nguyên là các số hữu tỉ
Xem thêm chi tiết các phương án giải toán 7 cánh diều trang 10 khác
Bài 4 trang 10
Các điểm A, B, C, D biểu diễn lần lượt các số: \(- \frac{9}{7}; - \frac{3}{7};\frac{2}{7};\frac{6}{7}\)
Bài 5 trang 10
Số đối của các số \(\frac{9}{{25}};\,\frac{{ - 8}}{{27}};\, - \frac{{15}}{{31}};\frac{5}{{ - 6}};\,3,9;\, - 12,5\) lần lượt là:
\(- \frac{9}{{25}};\,\frac{8}{{27}};\,\frac{{15}}{{31}};\frac{5}{6};\, - 3,9;\,12,5\)
Bài 6 trang 10

Bài 7 trang 10
a) \(2,4 = \frac{{12}}{5}\) và \(2\frac{3}{5} = \frac{{13}}{5}\)
Ta có: \(\frac{{12}}{5} < \frac{{13}}{5} \Rightarrow 2,4 < 2\frac{3}{5}\)
b) \(- 0,12 = -\frac{12}{100}= - \frac{3}{{25}}\) và \(- \frac{2}{5} = - \frac{{10}}{{25}}\)
Ta có: \(-3 > -10\) nên \(- \frac{3}{{25}} > - \frac{{10}}{{25}}\) nên \(- 0,12 > - \frac{2}{5}\)
c) \(\frac{{ - 2}}{7} = \frac{{ - 20}}{{70}}\) và \(- 0,3 = \frac{{ - 3}}{{10}} = \frac{{ - 21}}{{70}}\)
Do \(- 20 > -21\) nên \(\frac{{ - 20}}{{70}} > \frac{{ - 21}}{{70}}\) nên \(\frac{{ - 2}}{7} > - 0,3\)
Bài 8 trang 10
a) Ta có:
\(\begin{array}{l}\frac{{ - 3}}{7} = \frac{{ - 6}}{{14}} > \frac{{ - 7}}{{14}}= \frac{{ - 1}}{2} ;\\\,\frac{2}{5} = \frac{{14}}{{35}}\, > \frac{{10}}{{35}}=\frac{2}{7} \end{array}\)
Mà: \(\frac{{ - 7}}{{14}} < \frac{{ - 6}}{{14}} < \frac{{10}}{{35}} < \frac{{14}}{{35}}\)
=> Sắp xếp các số theo thứ tự tăng dần: \(\frac{{ - 1}}{2};\,\frac{{ - 3}}{7};\,\frac{2}{7};\frac{2}{5}\)
b) Ta có: \(\frac{{ - 5}}{6} = - 0,8\left( 3 \right)\)
Mà \(- 0,75 > - 0,8\left( 3 \right) > - 1 > - 4,5\)
=>Sắp xếp các số theo thứ tự giảm dần: \(- 0,75;\frac{{ - 5}}{6}; - 1; - 4,5\)
Bài 9 trang 10
Ta thấy mỗi vạch tương ứng 200g, chiếc kim chỉ quá số 47 một vạch rưỡi nên nó chỉ số 47,3kg
Vậy bạn Dương đọc đúng, bạn Minh và Quân đọc sai.
Bài 10 trang 10
Ta có: \(\frac{{13}}{5} = \frac{{26}}{{10}} = 2,6\)
Ta thấy \(2,75 > 2,6\) nên số đo chiều cao của tầng hầm được chọn là: 2,75m
Xem chi tiết hơn các phương án giải bài tập Toán 7 cánh diều trang 11
Trên đây là lý thuyết trọng tâm và giải bài tập SGK bài Tập hợp Q các số hữu tỉ được Đọc Tài Liệu biên soạn, Chúc bạn luôn học tốt và đạt được nhiều kết quả cao trong học tập.
Hướng dẫn giải Toán 7 bởi Đọc Tài Liệu