Ta giả sử 1 đơn vị trên trục Ou là 1 V, 1 đơn vị trên trục Ot là 1 s.
Chu kì dao động là 12 s.
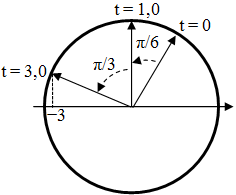
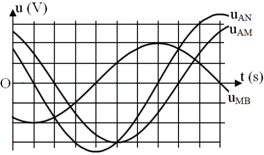
Xét u$_{AM}$: tại t = 0 đến t = 2,0 s dao động qua VTCB theo chiều âm → u$_{AM}$ = 3cos(ωt + π/6).
Xét u$_{MB}$: tại t = 0 đến t = 1,0 s dao động qua vị trí biên âm → u$_{MB}$ = 2cos(ωt + 5π/6).
Xét u$_{AN}$: tại t = 0 đến t = 1,0 s dao động qua VTCB theo chiều âm → pha ban đầu là π/3.
tại t = 1,0 s vật qua VTCB theo chiều âm đếm t = 3,0 s, vật qua vị trí −3 V và đang giảm. Nên u$_{AN}$ = 2$\sqrt 3 $cos(ωt + π/3).
Vậy: $\frac{{{Z_L}}}{{{Z_C}}} = \left| {\frac{{{u_{NB}}}}{{{u_{AM}}}}} \right| = \left| {\frac{{{u_{AM}} + {u_{MB}} - {u_{AN}}}}{{{u_{AM}}}}} \right| = \left| {\frac{{3\angle \frac{\pi }{6} + 2\angle \frac{{5\pi }}{6} - 2\sqrt 3 \angle \frac{\pi }{3}}}{{3\angle \frac{\pi }{6}}}} \right| = \frac{1}{3}$.
Cho mạch điện AMNB, trong đó giữa A và M, giữa M và N, giữa N và B lần lượt là
Xuất bản: 24/08/2020 - Cập nhật: 19/10/2023 - Tác giả: Chu Huyền
Câu Hỏi:
Đáp án và lời giải
Đặt điện áp xoay chiều vào hai đầu đoạn mạch có R, L, C mắc nối tiếp thì cảm kháng và dung kháng của đoạn mạch lần lượt là $Z_L$ và $Z_C$. Điện áp giữa hai đầu đoạn mạch sớm pha hơn cường độ dòng điện trong mạch khi
Khi $ Z_{L}>Z_{C}$ thì mạch có tính cảm kháng
$\tan \varphi_{u, i}=\dfrac{Z_{L}-Z_{C}}{R}>0 \Rightarrow \varphi_{u, i}=\varphi_{u}-\varphi_{i}>0 \Rightarrow \varphi_{u}>\varphi_{i}$
Đặt điện áp xoay chiều vào hai đầu đoạn mạch gồm điện trở 20 Ω mắc nối tiếp với cuộn cảm thuần thì cảm kháng của đoạn mạch là 30 Ω. Độ lệch pha của điện áp hai đầu đoạn mạch so với cường độ dòng điện trong mạch là
$\tan \varphi=\frac{Z_{L}}{R} \Leftrightarrow \varphi=\arctan \left(\frac{30}{20}\right)=0,983(\mathrm{rad})$
Cho đoạn mạch gồm điện trở thuần R, cuộn dây thuần cảm L và tụ điện C mắc nối tiếp như hình vẽ. Nếu đặt điện áp xoay chiều $u = {U_0}\cos ({\rm{\omega }}.t)$ vào hai điểm A, M thì thấy cường độ dòng điện qua mạch sớm pha $\dfrac{{\rm{\pi }}}{{\rm{4}}}$ rad so với điện áp trong mạch. Nếu đặt điện áp...
Lần 1: mạch chỉ R và C nối tiếp thì: $\tan (\dfrac{{ - \pi }}{4}) = \dfrac{{ - {Z_C}}}{R} = > {Z_C} = R\quad (1)$
Lần 2: Mạch có RLC mắc nối tiếp thì $\tan (\dfrac{\pi }{4}) = \dfrac{{{Z_L} - {Z_C}}}{R} = 1\quad (2)$
Từ (1) và (2) => ${Z_L} = 2{Z_C}$
Đặt một điện áp xoay chiều vào hai đầu một đoạn mạch gồm điện trở R mắc nối tiếp với cuộn cảm thuần thì cảm kháng và tổng trở của đoạn mạch lần lượt là $Z_{L}$ và Z. Hệ số công suất của đoạn mạch là
Hệ số công suất của mạch điện RLC mắc nối tiếp là $\cos \varphi=\frac{R}{Z}$
Đặt điện áp xoay chiều $u=U \sqrt{2} \cos \omega t(\omega>0)$ vào hai đầu một cuộn cảm thuần có độ tự cảm L thì cảm kháng của cuộn cảm là
Cảm kháng của cuộn cảm thuần có độ tự cảm L là $Z_{{L}}=\omega L$
Đặt điện áp xoay chiều vào hai đầu đoạn mạch gốm điện trở R mắc nối tiếp với cuộn cảm thuần thì cảm kháng và tổng trở của đoạn mạch lần lượt là $Z_L$ và $Z$. Hệ số công suất của đoạn mạch là cosφ. Công thức nào sau đây đúng?
Hệ số công suất của đoạn mạch là $cosφ = \dfrac{R}{Z}$
Đặt điện áp xoay chiều có tần số 50 Hz vào hai đầu cuộn cảm thuần có độ tự cảm $\frac{0,2}{\pi}$ H. Cảm kháng của cuộn cảm có giá trị là?
Cảm kháng của cuộn cảm có giá trị là: 20$\Omega$.
Một đoạn mạch xoay chiều RLC mắc nối tiếp, trong đó có các đại lượng R, L, C và điện áp hiệu dụng giữa hai đầu đoạn mạch U không thay đổi. Khi thay đổi tần số góc đến giá trị ${\omega _1}$ và ${\omega _2}$ tương ứng với các giá trị cảm kháng là 40 và 250 thì cường độ dòng điện hiệu dụng có giá trị bằng .....
Theo bài ra ta có ${I_1} = {I_2} \to {Z_1} = {Z_2}$
→$\left| {{Z_{{L_1}}} - {Z_{C{}_1}}} \right| = \left| {{Z_{{L_2}}} - {Z_{{C_2}}}} \right|\,\, \Rightarrow \,\,{Z_{{L_1}}} - {Z_{{C_1}}} = {Z_{{C_2}}} - {Z_{{L_2}}}\,\, \Rightarrow \,\,{Z_{{L_1}}} + {Z_{{L_2}}} = {Z_{{C_1}}} + {Z_{{C_2}}} = 40 + 250 = 290\left( \Omega \right)$ (1)
Đặt điện áp xoay chiều vào hai đầu đoạn mạch gồm điện trở R, cuộn cảm thuần và tụ điện mắc nối tiếp thì cảm kháng và dung kháng của đoạn mạch lần lượt là $Z_{L}$ và $Z_{C}$. Tổng trở Z của đoạn mạch được tính bằng công thức nào sau đây?
Tổng trở Z của đoạn mạch được tính bằng công thức: $Z = \sqrt{R^{2}+(Z_{L} - Z_{C})^{2}}$
Dung kháng của một mạch RLC nối tiếp đang có giá trị nhỏ hơn cảm kháng. Muốn xảy ra hiện tượng cộng hưởng điện trong mạch, ta cần điều chỉnh theo hướng
Do hiện tại ωL > 1/(ωC) → để xảy ra cộng hưởng cần giảm ω (tức giảm f).
