Có bao nhiêu số nguyên x để giá trị của đa thức A = 2x3 - 3x2 + 2x + 2 chia hết cho giá trị của đa thức B = x2 + 1

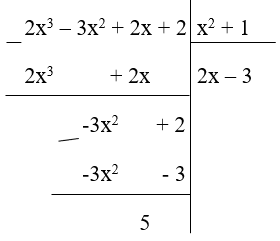
Ta có A : B
Để giá trị của đa thức A = ${2}{x}^3 - {3}{x}^2$ + 2x + 2 chia hết cho giá trị của đa thức B = ${x}^2$+ 1 thì
5 ⁝ (${x}^2$ + 1)
Hay (${x}^2$ + 1) Є U(5) = {-1; 1; -5; 5}
+) ${x}^2$ + 1 = -1
$\Leftrightarrow$ ${x}^2$ = -2 (VL)
+) ${x}^2$+ 1 = 1
$\Leftrightarrow$${x}^2$ = 0
$\Leftrightarrow$ x = 0 (tm)
+) ${x}^2$ + 1 = -5
$\Leftrightarrow$${x}^2$ = -6 (VL)
+) ${x}^2$ + 1 = 5
$\Leftrightarrow$${x}^2$ = 4
$\Leftrightarrow$x = ± 2 ™
Vậy có 3 giá trị của x thỏa mãn đề bài là x = 0; x = -2; x = 2
Đáp án cần chọn là: A