Bài 1 trang 20 Toán 7 Cánh Diều tập 1
Câu hỏi
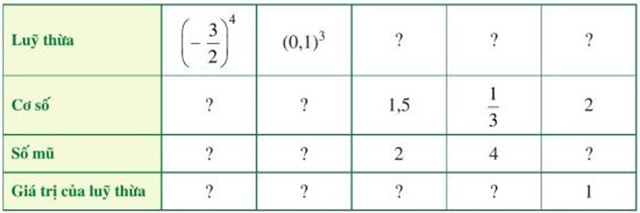
Tìm số thích hợp cho “?” trong bảng sau:
Bài giải
| Lũy thừa | \({\left( {\frac{{ - 3}}{2}} \right)^4}\) | \({\left( {0,1} \right)^3}\) | \({\left( {1,5} \right)^2}\) | \({\left( {\frac{1}{3}} \right)^4}\) | \({2^0}\) |
|---|---|---|---|---|---|
| Cơ số | \(\frac{{ - 3}}{2}\) | \(0,1\) | \(1,5\) | \(\frac{1}{3}\) | 2 |
| Số mũ | 4 | \(3\) | \(2\) | 4 | 0 |
| Giá trị lũy thừa | \(\frac{{81}}{{16}}\) | \(0,001\) | \(2,25\) | \(\frac{1}{{81}}\) | 1 |
Bài 2 trang 20 Toán 7 Cánh Diều tập 1
Câu hỏi
So sánh:
a) \({( - 2)^4} \cdot {( - 2)^5}\) và \({( - 2)^{12}}:{( - 2)^3};\)
b) \( {\left( {\frac{1}{2}} \right)^2} \cdot {\left( {\frac{1}{2}} \right)^6}\) và \({\left[ {{{\left( {\frac{1}{2}} \right)}^4}} \right]^2}\)
c) \({(0,3)^8}:{(0,3)^2}\) và \({\left[ {{{(0,3)}^2}} \right]^3}\)
d) \({\left( { - \frac{3}{2}} \right)^5}:{\left( { - \frac{3}{2}} \right)^3}\) và \({\left( {\frac{3}{2}} \right)^2}.\)
Bài giải
a) \({( - 2)^4} \cdot {( - 2)^5} = {\left( { - 2} \right)^{4 + 5}} = {\left( { - 2} \right)^9}\)
\( {( - 2)^{12}}:{( - 2)^3} = {\left( { - 2} \right)^{12 - 3}} = {\left( { - 2} \right)^9}\)
Vậy \({( - 2)^4} \cdot {( - 2)^5} = {( - 2)^{12}}:{( - 2)^3};\)
b) \({\left( {\frac{1}{2}} \right)^2} \cdot {\left( {\frac{1}{2}} \right)^6} = {\left( {\frac{1}{2}} \right)^{2 + 6}} = {\left( {\frac{1}{2}} \right)^8}\)
\({\left[ {{{\left( {\frac{1}{2}} \right)}^4}} \right]^2} = {\left( {\frac{1}{2}} \right)^{4.2}} = {\left( {\frac{1}{2}} \right)^8}\)
Vậy \({\left( {\frac{1}{2}} \right)^2} \cdot {\left( {\frac{1}{2}} \right)^6} = {\left[ {{{\left( {\frac{1}{2}} \right)}^4}} \right]^2}\)
c) \( {(0,3)^8}:{(0,3)^2} = {\left( {0,3} \right)^{8 - 2}} = {\left( {0,3} \right)^6}\)
\({\left[ {{{(0,3)}^2}} \right]^3} = {\left( {0,3} \right)^{2.3}} = {\left( {0,3} \right)^6}\)
Vậy \({(0,3)^8}:{(0,3)^2}= {\left[ {{{(0,3)}^2}} \right]^3}.\)
d) \({\left( { - \frac{3}{2}} \right)^5}:{\left( { - \frac{3}{2}} \right)^3} = {\left( { - \frac{3}{2}} \right)^{5 - 3}} = {\left( { - \frac{3}{2}} \right)^2} = {\left( {\frac{3}{2}} \right)^2}\)
Vậy \( {\left( { - \frac{3}{2}} \right)^5}:{\left( { - \frac{3}{2}} \right)^3} = {\left( {\frac{3}{2}} \right)^2}.\)
Bài 3 trang 20 Toán 7 Cánh Diều tập 1
Câu hỏi
Tìm x, biết:
a) \({(1,2)^3}.x = {(1,2)^5};\)
b) \({\left( {\frac{2}{3}} \right)^7}:x = {\left( {\frac{2}{3}} \right)^6}\)
Bài giải
a)
\(\begin{array}{l}{(1,2)^3}.x = {(1,2)^5}\\x = {(1,2)^5}:{(1,2)^3}\\x = {(1,2)^2}\\x = 1,44\end{array}\)
Vậy \(x = 1,44.\)
b)
\(\begin{array}{l}{\left( {\frac{2}{3}} \right)^7}:x = {\left( {\frac{2}{3}} \right)^6}\\x = {\left( {\frac{2}{3}} \right)^7}:{\left( {\frac{2}{3}} \right)^6}\\x = \frac{2}{3}\end{array}\)
Vậy \(x = \frac{2}{3}.\)
Bài 4 trang 20 Toán 7 Cánh Diều tập 1
Câu hỏi
Viết kết quả mỗi phép tính sau dưới dạng luỹ thừa của \(a\) :
a) \({\left( {\frac{8}{9}} \right)^3} \cdot \frac{4}{3} \cdot \frac{2}{3}\) với \(a = \frac{8}{9}\);
b) \({\left( {\frac{1}{4}} \right)^7} \cdot 0,25\) với \(a = 0,25\);
c) \({( - 0,125)^6}:\frac{{ - 1}}{8}\) với \(a = - \frac{1}{8};\)
d) \({\left[ {{{\left( {\frac{{ - 3}}{2}} \right)}^3}} \right]^2} \) với \(a = \frac{{ - 3}}{2}\).
Bài giải
a) \({\left( {\frac{8}{9}} \right)^3} \cdot \frac{4}{3} \cdot \frac{2}{3} = {\left( {\frac{8}{9}} \right)^3}.\frac{8}{9} = {\left( {\frac{8}{9}} \right)^4}=a^4\)
b) \({\left( {\frac{1}{4}} \right)^7} \cdot 0,25 = {\left( {0,25} \right)^7}.0,25 = {\left( {0,25} \right)^8}=a^8\)
c) \({( - 0,125)^6}:\frac{{ - 1}}{8} = {\left( {\frac{{ - 1}}{8}} \right)^6}:\frac{{ - 1}}{8} = {\left( {\frac{{ - 1}}{8}} \right)^5}=a^5\)
d) \({\left[ {{{\left( {\frac{{ - 3}}{2}} \right)}^3}} \right]^2} = {\left( {\frac{{ - 3}}{2}} \right)^{3.2}} = {\left( {\frac{{ - 3}}{2}} \right)^6}=a^6\)
Bài 5 trang 20 Toán 7 Cánh Diều tập 1
Câu hỏi
Cho x là số hữu tỉ. Viết \({x^{12}}\) dưới dạng:
a) Luỹ thừa của \({x^2}\);
b) Luỹ thừa của\( {x^3}\).
Bài giải
a) \({x^{12}} = {x^{2.6}} = {\left( {{x^2}} \right)^6}\)
b) \({x^{12}} = {x^{3.4}} = {\left( {{x^3}} \right)^4}\)
Bài 6 trang 20 Toán 7 Cánh Diều tập 1
Câu hỏi
Trên bản đồ có tỉ lệ 1: 100 000, một cánh đồng lúa có dạng hình vuông với độ dài cạnh là \(0,7\;{\rm{cm}}\). Tính diện tích thực tế theo đơn vị mét vuông của cánh đồng lúa đó (viết kết quả dưới dạng \(a{.10^n}\) với \(1 \le a < 10 )\)
Bài giải
Độ dài cạnh hình vuông ngoài thực tế là: \(0,7. 100 000 = 70 000 (cm) = 700 (m)\)
Diện tích cánh đồng lúa hình vuông ngoài thực tế là: \({\left( {700} \right)^2} = 490\,000 (m2) = 4,{9.10^5} (m2)\)
Bài 7 trang 20 Toán 7 Cánh Diều tập 1
Câu hỏi
Biết vận tốc ánh sáng xấp xỉ bằng \(299\,792\,458\;{\rm{m/s}}\) và ánh sáng Mặt Trời cần khoảng 8 phút 19 giây mới đến được Trái Đất. (Nguồn: https://vi.wikipedia.org)
Khoảng cách giữa Mặt Trời và Trái Đất xấp xỉ bằng bao nhiêu ki-lô-mét?
Bài giải
Ta có: \(299\,792\,458\; \approx {\rm{300}}\,{\rm{000}}\,{\rm{000 = 3}}{\rm{.1}}{{\rm{0}}^8}(m/s)\)
Đổi 8 phút 19 giây = 499 giây \( \approx\) 500 giây
Khoảng cách giữa Mặt Trời và Trái Đất là:
\({3.10^8}.500 = {3.10^8}{.5.10^2} = {15.10^{10}}(m) = {15.10^7}(km)\)
Bài tiếp theo: Toán 7 Cánh Diều trang 21
Xem thêm
- Toán 7 cánh diều trang 10
- Toán 7 cánh diều trang 11
- Toán 7 cánh diều trang 16
- Toán 7 cánh diều trang 25
- Toán 7 cánh diều trang 26
- Toán 7 cánh diều trang 29
- Toán 7 cánh diều trang 30
- Toán 7 cánh diều trang 31
Trên đây là chi tiết hướng dẫn Giải bài tập Toán 7 Cánh Diều trang 20 được Đọc Tài Liệu biên soạn với mong muốn hỗ trợ các em học sinh học tốt hơn môn Toán lớp 7
Hướng dẫn giải Toán 7 Cánh Diều bởi Đọc Tài Liệu